某一跨度为6.6m承受均布荷载的矩形截面钢筋混凝土梁,截面尺寸为300mm×550mm,γ =1.0,混凝土强度等级C20,纵向受力钢筋采用HRB335级钢筋,箍筋采用HPB235级钢筋,h
=1.0,混凝土强度等级C20,纵向受力钢筋采用HRB335级钢筋,箍筋采用HPB235级钢筋,h =510mm;在支座处的剪力设计值为V=55.9kN,对应的扭矩设计值为T=17.88kN·m。问其箍筋和受扭纵向钢筋的配置下列哪一组值最为合理?(提示:ζ--受扭的纵向钢筋与箍筋的配筋强度比值,取ζ=1.2。)
=510mm;在支座处的剪力设计值为V=55.9kN,对应的扭矩设计值为T=17.88kN·m。问其箍筋和受扭纵向钢筋的配置下列哪一组值最为合理?(提示:ζ--受扭的纵向钢筋与箍筋的配筋强度比值,取ζ=1.2。)
 =1.0,混凝土强度等级C20,纵向受力钢筋采用HRB335级钢筋,箍筋采用HPB235级钢筋,h
=1.0,混凝土强度等级C20,纵向受力钢筋采用HRB335级钢筋,箍筋采用HPB235级钢筋,h =510mm;在支座处的剪力设计值为V=55.9kN,对应的扭矩设计值为T=17.88kN·m。问其箍筋和受扭纵向钢筋的配置下列哪一组值最为合理?(提示:ζ--受扭的纵向钢筋与箍筋的配筋强度比值,取ζ=1.2。)
=510mm;在支座处的剪力设计值为V=55.9kN,对应的扭矩设计值为T=17.88kN·m。问其箍筋和受扭纵向钢筋的配置下列哪一组值最为合理?(提示:ζ--受扭的纵向钢筋与箍筋的配筋强度比值,取ζ=1.2。) 正确答案:
B
答案解析:
【主要解答过程如下】:(1)按矩形截面验算截面控制条件。根据《混凝土结构设计规范》7.6.1条,
h /b=510/300=1.7<4故截面控制条件为:
/b=510/300=1.7<4故截面控制条件为:
V/bh +T/0.8W
+T/0.8W ≤0.25β
≤0.25β f
f
根据规范7.6.3条
W =b
=b /6(3h-b)=300
/6(3h-b)=300 (3×550-300)=2025×10
(3×550-300)=2025×10 mm
mm
将W 及有关数据代入上式得:55900/300×510+17880000/0.8×2025×10
及有关数据代入上式得:55900/300×510+17880000/0.8×2025×10 =0.365+1.104=1.469N/mm
=0.365+1.104=1.469N/mm <0.25×1.0×9.6=2.4N/mm
<0.25×1.0×9.6=2.4N/mm
(2)验算受剪扭承载力计算条件。
依据规范7.6.2条
V/bh +T/W
+T/W =0.365+17880000/2025×10
=0.365+17880000/2025×10 =1.25N/mm
=1.25N/mm >0.7f
>0.7f =0.7×1.1=0.77N/mm
=0.7×1.1=0.77N/mm
应进行受剪扭承载力计算。
又从7.6.11条
0.35f bh
bh =0.35×1.1×300×510=58905N>V=55900N
=0.35×1.1×300×510=58905N>V=55900N
故可仅按受弯构件的正截面受弯承载力和纯扭构件的受扭承载力分别进行计算。
(3)按规范10.2.12条,梁剪扭箍筋的配筋率不应小于0.28f /f
/f 。
。
ρ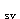 =A
=A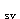 /bs≥0.28×1.1/210=0.00147
/bs≥0.28×1.1/210=0.00147
A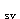 /s≥300×0.00147=0.44mm
/s≥300×0.00147=0.44mm
(4)根据规范7.6.4条,矩形截面纯扭构件的受扭承载力应按下列公式计算:
T≤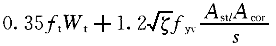 (3-10-1)式中
(3-10-1)式中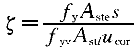 (3-10-2)
(3-10-2)
又从10.2.5条,梁内受扭纵向钢筋的配筋率应符合下列规定:
 (3-10-3)
(3-10-3)
T/V =17880000/55900×300=1.07
=17880000/55900×300=1.07
A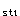 ≥0.6×
≥0.6×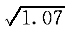 ×(1.1/300)×300×550=376mm
×(1.1/300)×300×550=376mm
A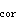 =490×240=117600mm
=490×240=117600mm
u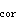 =2×(490+240)=1460mm
=2×(490+240)=1460mm
因已规定ζ=1.20,将有关数值代入式(3-10-1)得:17880000=0.35×1.1×2025×10 +
+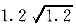 ×210×A
×210×A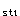 ×117600/s
×117600/s
解出A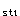 /s=0.3106,A
/s=0.3106,A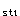 =0.3106S
=0.3106S
从式(3-10-2),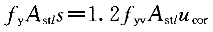
300×A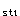 =1.2×210×0.3106×1460
=1.2×210×0.3106×1460
A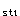 =381mm
=381mm >376mm
>376mm ,采用381mm
,采用381mm
(5)箍筋配置计算。
根据规范表10.2.10,可取φ6@350
受剪构造箍筋每延米的用量为28.3×2/0.35=161.71mm
受扭箍筋每延米的用量为2×0.31065×(100/s)=621.3mm
总计每延米箍筋用量161.71+621.3=783.01mm
选用φ8@120双肢箍,
A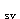 =2×50.3=100.6mm
=2×50.3=100.6mm >0.44×120=52.8mm
>0.44×120=52.8mm
且100.6×(1000/120)=838.3mm >783.01mm
>783.01mm
符合要求,因此选项B是正确的。
【点评】:(1)在上述计算中ζ取用1.20,这是因为根据规范7.6.4条条文说明,当ζ=1.20左右时为钢筋达到屈服的最佳值。
(2)梁的纵向受力钢筋不仅有按受扭计算所需的钢筋,还有按正截面受弯承载力计算所需的钢筋,在设计上的一般做法是将这两者叠加。对简支梁及连续梁来说,这种处理方式是偏于保守的,这是因为梁的扭矩最大值通常是在支座截面处,但此处梁的正弯矩为零,从跨中延伸过来的正弯矩钢筋在此锚入支座,实际上并不需要这么多,完全可以利用其抗扭,可参见《混凝土结构设计规范算例》一书雨篷梁计算一节中。
(3)对抗震设计,规范未提供构件受扭构件的承载力计算公式,这是因为缺乏试验资料;为此建议读者今后在抗震设计中,尽量避免布置出现受扭构件。
h
 /b=510/300=1.7<4故截面控制条件为:
/b=510/300=1.7<4故截面控制条件为:V/bh
 +T/0.8W
+T/0.8W ≤0.25β
≤0.25β f
f
根据规范7.6.3条
W
 =b
=b /6(3h-b)=300
/6(3h-b)=300 (3×550-300)=2025×10
(3×550-300)=2025×10 mm
mm
将W
 及有关数据代入上式得:55900/300×510+17880000/0.8×2025×10
及有关数据代入上式得:55900/300×510+17880000/0.8×2025×10 =0.365+1.104=1.469N/mm
=0.365+1.104=1.469N/mm <0.25×1.0×9.6=2.4N/mm
<0.25×1.0×9.6=2.4N/mm
(2)验算受剪扭承载力计算条件。
依据规范7.6.2条
V/bh
 +T/W
+T/W =0.365+17880000/2025×10
=0.365+17880000/2025×10 =1.25N/mm
=1.25N/mm >0.7f
>0.7f =0.7×1.1=0.77N/mm
=0.7×1.1=0.77N/mm
应进行受剪扭承载力计算。
又从7.6.11条
0.35f
 bh
bh =0.35×1.1×300×510=58905N>V=55900N
=0.35×1.1×300×510=58905N>V=55900N故可仅按受弯构件的正截面受弯承载力和纯扭构件的受扭承载力分别进行计算。
(3)按规范10.2.12条,梁剪扭箍筋的配筋率不应小于0.28f
 /f
/f 。
。ρ
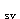 =A
=A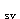 /bs≥0.28×1.1/210=0.00147
/bs≥0.28×1.1/210=0.00147A
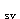 /s≥300×0.00147=0.44mm
/s≥300×0.00147=0.44mm(4)根据规范7.6.4条,矩形截面纯扭构件的受扭承载力应按下列公式计算:
T≤
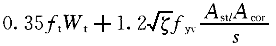 (3-10-1)式中
(3-10-1)式中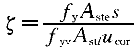 (3-10-2)
(3-10-2)又从10.2.5条,梁内受扭纵向钢筋的配筋率应符合下列规定:
 (3-10-3)
(3-10-3)T/V
 =17880000/55900×300=1.07
=17880000/55900×300=1.07A
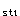 ≥0.6×
≥0.6×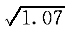 ×(1.1/300)×300×550=376mm
×(1.1/300)×300×550=376mm
A
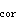 =490×240=117600mm
=490×240=117600mm
u
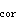 =2×(490+240)=1460mm
=2×(490+240)=1460mm因已规定ζ=1.20,将有关数值代入式(3-10-1)得:17880000=0.35×1.1×2025×10
 +
+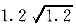 ×210×A
×210×A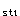 ×117600/s
×117600/s解出A
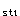 /s=0.3106,A
/s=0.3106,A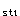 =0.3106S
=0.3106S从式(3-10-2),
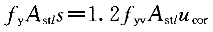
300×A
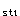 =1.2×210×0.3106×1460
=1.2×210×0.3106×1460A
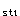 =381mm
=381mm >376mm
>376mm ,采用381mm
,采用381mm
(5)箍筋配置计算。
根据规范表10.2.10,可取φ6@350
受剪构造箍筋每延米的用量为28.3×2/0.35=161.71mm

受扭箍筋每延米的用量为2×0.31065×(100/s)=621.3mm

总计每延米箍筋用量161.71+621.3=783.01mm

选用φ8@120双肢箍,
A
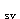 =2×50.3=100.6mm
=2×50.3=100.6mm >0.44×120=52.8mm
>0.44×120=52.8mm
且100.6×(1000/120)=838.3mm
 >783.01mm
>783.01mm
符合要求,因此选项B是正确的。
【点评】:(1)在上述计算中ζ取用1.20,这是因为根据规范7.6.4条条文说明,当ζ=1.20左右时为钢筋达到屈服的最佳值。
(2)梁的纵向受力钢筋不仅有按受扭计算所需的钢筋,还有按正截面受弯承载力计算所需的钢筋,在设计上的一般做法是将这两者叠加。对简支梁及连续梁来说,这种处理方式是偏于保守的,这是因为梁的扭矩最大值通常是在支座截面处,但此处梁的正弯矩为零,从跨中延伸过来的正弯矩钢筋在此锚入支座,实际上并不需要这么多,完全可以利用其抗扭,可参见《混凝土结构设计规范算例》一书雨篷梁计算一节中。
(3)对抗震设计,规范未提供构件受扭构件的承载力计算公式,这是因为缺乏试验资料;为此建议读者今后在抗震设计中,尽量避免布置出现受扭构件。
