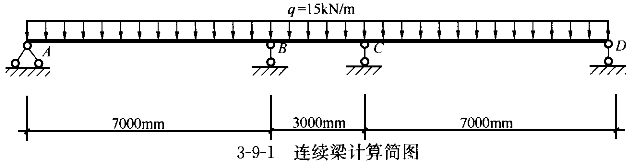
图3-9-1所示钢筋混凝土连续梁,梁截面尺寸250mm×500mm,混凝土强度等级C25;全部荷载(含自重)为g=15kN/m,采用最简单的弯矩分配法(利用对称法)求AB跨跨中最大弯矩。

正确答案:
D
答案解析:
【主要解答过程如下】:(1)求分配系数
设梁的截面刚度为EI。
AB跨及CD跨梁的线刚度i =i
=i =EI/7×(3/4)=(3/28)EI(梁的一端为铰接,乘以修正系数3/4)
=EI/7×(3/4)=(3/28)EI(梁的一端为铰接,乘以修正系数3/4)
BC跨的线刚度i =EI/3×(1/2)=(1/6)EI(考虑梁及其荷载的对称性,乘以修正系数1/2)
=EI/3×(1/2)=(1/6)EI(考虑梁及其荷载的对称性,乘以修正系数1/2)
则节点B及C的分配系数为:
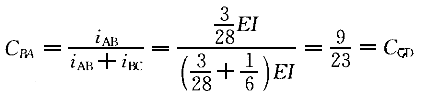
C =1-9/23=14/23=C
=1-9/23=14/23=C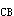
(2)求AB跨跨中最大弯矩
梁固端弯矩:
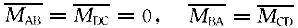 =-(1/8)×15×7
=-(1/8)×15×7 =-91.875kN·m
=-91.875kN·m
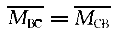 =-(1/12)×15×3
=-(1/12)×15×3 =-11.25kN·m
=-11.25kN·m
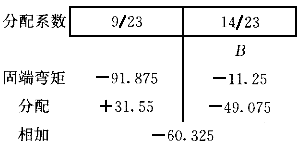
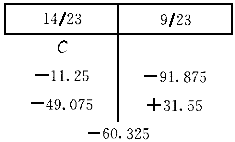
求AB跨跨中最大弯矩时计算简图见图3-9-2。
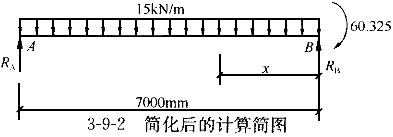
R =(2/7)×15+(60.325/7)=61.12Kn
=(2/7)×15+(60.325/7)=61.12Kn
M =61.12x-(1/2)×15x
=61.12x-(1/2)×15x -60.325
-60.325
dM /dx=0,x=61.12/15=4.075m
/dx=0,x=61.12/15=4.075m
M =61.12×4.075-(1/2)×15×4.075
=61.12×4.075-(1/2)×15×4.075 -60.325=64.21kN·m
-60.325=64.21kN·m
故选项D是对的。A则忘记减去支座弯矩值62.325kN·m;B为跨度中点的弯矩值,但并非最大弯矩;C是在选项B的基础上忘记减去支座弯矩。
【点评】:本题纯属结构力学的计算问题。对于刚度对称、荷载对称的连续梁,当为奇数跨数时,中间跨的转角必定相等,在此条件下只要把中间跨的线刚度乘以1/2,就可以用上述简化方法求解;当跨数为偶数时,在对称轴线上的支座处,转角必定为零,相当于梁嵌固于此轴线上的支座处,于是只要取出连续梁的一半,按具有固定端的连续梁计算即可(图3-9-3)。

设梁的截面刚度为EI。
AB跨及CD跨梁的线刚度i
 =i
=i =EI/7×(3/4)=(3/28)EI(梁的一端为铰接,乘以修正系数3/4)
=EI/7×(3/4)=(3/28)EI(梁的一端为铰接,乘以修正系数3/4)BC跨的线刚度i
 =EI/3×(1/2)=(1/6)EI(考虑梁及其荷载的对称性,乘以修正系数1/2)
=EI/3×(1/2)=(1/6)EI(考虑梁及其荷载的对称性,乘以修正系数1/2)则节点B及C的分配系数为:
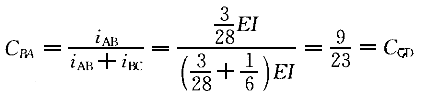
C
 =1-9/23=14/23=C
=1-9/23=14/23=C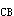
(2)求AB跨跨中最大弯矩
梁固端弯矩:
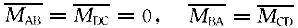 =-(1/8)×15×7
=-(1/8)×15×7 =-91.875kN·m
=-91.875kN·m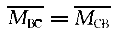 =-(1/12)×15×3
=-(1/12)×15×3 =-11.25kN·m
=-11.25kN·m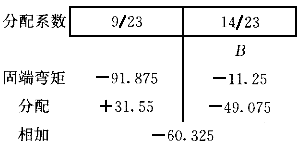
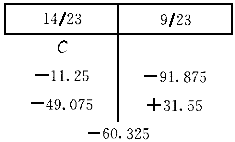
求AB跨跨中最大弯矩时计算简图见图3-9-2。

R
 =(2/7)×15+(60.325/7)=61.12Kn
=(2/7)×15+(60.325/7)=61.12KnM
 =61.12x-(1/2)×15x
=61.12x-(1/2)×15x -60.325
-60.325dM
 /dx=0,x=61.12/15=4.075m
/dx=0,x=61.12/15=4.075mM
 =61.12×4.075-(1/2)×15×4.075
=61.12×4.075-(1/2)×15×4.075 -60.325=64.21kN·m
-60.325=64.21kN·m故选项D是对的。A则忘记减去支座弯矩值62.325kN·m;B为跨度中点的弯矩值,但并非最大弯矩;C是在选项B的基础上忘记减去支座弯矩。
【点评】:本题纯属结构力学的计算问题。对于刚度对称、荷载对称的连续梁,当为奇数跨数时,中间跨的转角必定相等,在此条件下只要把中间跨的线刚度乘以1/2,就可以用上述简化方法求解;当跨数为偶数时,在对称轴线上的支座处,转角必定为零,相当于梁嵌固于此轴线上的支座处,于是只要取出连续梁的一半,按具有固定端的连续梁计算即可(图3-9-3)。

