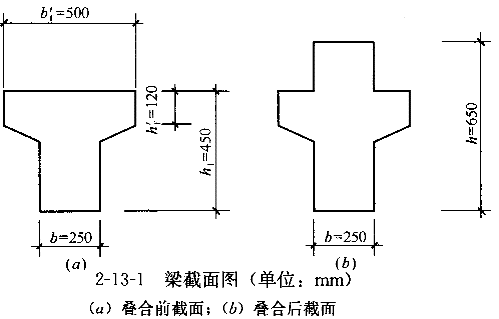
某装配整体式单跨框架结构,结构完全对称,跨度6m,采用钢筋混凝土叠合梁和预制板方案,叠合梁截面如图2-13-1所示,承受均布荷载;梁宽b=250mm,预制梁截面高度h =450mm,b′
=450mm,b′ =500mm,h′
=500mm,h′ =120mm,叠合梁高h=650mm;纵向受拉钢筋采用HRB400级钢筋,混凝土采用C30(含叠合层);施工阶段不加支撑。
=120mm,叠合梁高h=650mm;纵向受拉钢筋采用HRB400级钢筋,混凝土采用C30(含叠合层);施工阶段不加支撑。
 =450mm,b′
=450mm,b′ =500mm,h′
=500mm,h′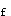 =120mm,叠合梁高h=650mm;纵向受拉钢筋采用HRB400级钢筋,混凝土采用C30(含叠合层);施工阶段不加支撑。
=120mm,叠合梁高h=650mm;纵向受拉钢筋采用HRB400级钢筋,混凝土采用C30(含叠合层);施工阶段不加支撑。
- 若预制梁、板及叠合层自重标准值为q
 =12kN/m,施工阶段活荷载标准值为q
=12kN/m,施工阶段活荷载标准值为q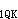 =6kN/m;使用阶段活荷载标准值为q
=6kN/m;使用阶段活荷载标准值为q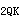 =24kN/m,新增的面层、吊顶等永久荷载标准值为q
=24kN/m,新增的面层、吊顶等永久荷载标准值为q ]=10kN/m;在使用阶段竖向荷载作用下梁的跨中最大正弯矩为M=0.6M
]=10kN/m;在使用阶段竖向荷载作用下梁的跨中最大正弯矩为M=0.6M ,式中M
,式中M 为按简支梁计算的跨中最大正弯矩。则第二阶段梁的跨中最大正弯矩设计值与支座负弯矩设计值与下列哪一组数值最为接近?A.225.72kN·m,82.08kN·mB.270kN·m,205kN·mC.187.92kN·m,82.08kN·mD.162kN·m,108kN·m
为按简支梁计算的跨中最大正弯矩。则第二阶段梁的跨中最大正弯矩设计值与支座负弯矩设计值与下列哪一组数值最为接近?A.225.72kN·m,82.08kN·mB.270kN·m,205kN·mC.187.92kN·m,82.08kN·mD.162kN·m,108kN·m - 若对跨中截面,M
 =60kN·m,M
=60kN·m,M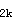 =M
=M +M
+M =120kN·m,梁底部配置的纵向受拉钢筋为4
=120kN·m,梁底部配置的纵向受拉钢筋为4 20,α
20,α =40mm,则在荷载效应的标准组合下,此钢筋的应力与下列哪一数值最为接近?A.313.9N/mm
=40mm,则在荷载效应的标准组合下,此钢筋的应力与下列哪一数值最为接近?A.313.9N/mm B.301.2N/mm
B.301.2N/mm C.323.1N/mm
C.323.1N/mm D.286.2N/mm
D.286.2N/mm
正确答案:
(1)C
(2)D
(2)D
答案解析:
第1小题:【主要解答过程如下】:(1)施工阶段如不加支撑,则在第一阶段后浇的叠合层混凝土未达到强度之前,荷载应由预制构件承受,此时预制构件应按简支梁计算。
M =1/8(q
=1/8(q ι
ι )=(1/8)×12×6
)=(1/8)×12×6 =54kN·m
=54kN·m
M =1/8(q
=1/8(q ι
ι )=(1/8)×6×6
)=(1/8)×6×6 =27kN·m
=27kN·m
(2)第二阶段:叠合层混凝土达到设计规定的强度后,叠合构件应按整体结构计算。对跨中截面:
M =0.6×(1/8)×10×6
=0.6×(1/8)×10×6 =27kN·m
=27kN·m
M =0.6×(1/8)×24×6
=0.6×(1/8)×24×6 =64.8kN·m
=64.8kN·m
于是在正弯矩区段,根据《混凝土结构设计规范》10.6.3条有:
M=1.2M +1.2M
+1.2M +1.4M
+1.4M =1.2×54+1.2×27+1.4×64.8=187.92kN·m
=1.2×54+1.2×27+1.4×64.8=187.92kN·m
在负弯矩区段,对支座截面:
M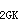 =(1-0.6)×(1/8)×10×6
=(1-0.6)×(1/8)×10×6 =18kN·m
=18kN·m
M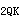 =(1-0.6)×(1/8)×24×6
=(1-0.6)×(1/8)×24×6 =43.2kN·m
=43.2kN·m
M=1.2M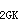 +1.4M
+1.4M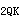 =1.2×18+1.4×43.2=82.08kN·m
=1.2×18+1.4×43.2=82.08kN·m
因此选项C是正确的。
选项B的错误在于对跨中截面及支座截面均取:M =(1/8)×10×6
=(1/8)×10×6 =45kN·m
=45kN·m
M =(1/8)×24×6
=(1/8)×24×6 =108kN·m这就得到:对跨中截面M=1.2×54+1.2×45+1.4×108=270kN·m
=108kN·m这就得到:对跨中截面M=1.2×54+1.2×45+1.4×108=270kN·m
对支座截面M=1.2×45+1.4×108=205kN·m
选项A的错误在于在选项B的基础上,将第一阶段施工活荷载产生的弯矩值亦加上。
选项D则是未考虑叠合构件的特点,按照整体结构计算所得结果。即:
对跨中截面M=1.2×0.6×(1/8)×(12+10)×6 +1.4×0.6×(1/8)×24×6
+1.4×0.6×(1/8)×24×6 =162kN·m
=162kN·m
对支座截面M=1.2×0.4×(1/8)×(12+10)×6 +1.4×0.4×(1/8)×24×6
+1.4×0.4×(1/8)×24×6 =108kN·m
=108kN·m
所以选项A、B、D都是不正确的。
【点评】:(1)叠合梁在20世纪60~70年代,为了节约木材,曾于我国工业与民用建筑工程中得到广泛的应用,也做了大量的试验研究工作。经验表明,当h /h<0.4时,应在施工阶段设置可靠的支撑,且h
/h<0.4时,应在施工阶段设置可靠的支撑,且h /h<0.4的二阶段受力叠合构件,其受力性能和经济效果均较差,裂缝及挠度很难满足使用要求。
/h<0.4的二阶段受力叠合构件,其受力性能和经济效果均较差,裂缝及挠度很难满足使用要求。
(2)试验表明,叠合构件的受弯承载力约有25%的试件达不到整体构件的受弯承载力,曾有专家建议将规范公式(10.6.3-2)改为:
正弯矩区段M=[1.7-0.7(h /h)]M
/h)]M +M
+M +M
+M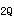
因此提请结构工程师注意,在设计叠合构件时正截面受弯承载力留有适当余地为好。
(3)规范10.6.3条对叠合构件的弯矩设计值作了如下规定:
正弯矩区段M=M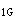 +M
+M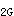 +M
+M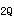
负弯矩区段M=M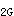 +M
+M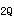
式中M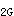 --第二阶段面层、吊顶等自重在计算截面产生的弯矩设计值;
--第二阶段面层、吊顶等自重在计算截面产生的弯矩设计值;
M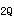 --第二阶段可变荷载在计算截面产生的弯矩设计值。
--第二阶段可变荷载在计算截面产生的弯矩设计值。
M 、M
、M 均应按整体结构计算,且跨中截面和支座截面一般为不同的数值。由于在正弯矩区段和负弯矩区段均采用同一符号表示,于是有些结构工程师便错误地理解为应取同一数值,这是不正确的,例如本题选项B便是如此。
均应按整体结构计算,且跨中截面和支座截面一般为不同的数值。由于在正弯矩区段和负弯矩区段均采用同一符号表示,于是有些结构工程师便错误地理解为应取同一数值,这是不正确的,例如本题选项B便是如此。
第1小题:【主要解答过程如下】:(1)A =1256mm
=1256mm (4
(4 20),根据《混凝土结构设计规范》式(10.6.8-3),在弯矩M
20),根据《混凝土结构设计规范》式(10.6.8-3),在弯矩M 作用下,预制构件纵向受拉钢筋的应力为:
作用下,预制构件纵向受拉钢筋的应力为:
σ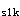 =M
=M /0.87A
/0.87A h
h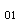 =60×10
=60×10 /0.87×1256×(450-40)=133.9N/mm
/0.87×1256×(450-40)=133.9N/mm
下面按T形截面计算预制构件的正截面受弯承载力设计值M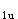 。
。
依据规范7.2.2条,f A
A =360×1256=452160N<α
=360×1256=452160N<α f
f b′
b′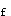 h′
h′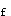 =1.0×14.3×500×120
=1.0×14.3×500×120
故应按宽度为500mm的矩形截面计算。
按规范7.2.1条,α f
f b′
b′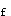 x=1.0×14.3×500x=f
x=1.0×14.3×500x=f A
A =360×1256=452160
=360×1256=452160
x=452160/1.0×14.3×500=63.24mm
M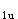 =α
=α f
f b′
b′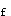 x=1.0×14.3×500×63.24×[410-(1/2)×63.24]=171.09×10
x=1.0×14.3×500×63.24×[410-(1/2)×63.24]=171.09×10 N·mm
N·mm
M =60kN·m>0.35M
=60kN·m>0.35M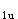 =0.35×171.09=59.88kN·m
=0.35×171.09=59.88kN·m
于是从10.6.8条,在弯矩M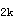 作用下叠合构件纵向受拉钢筋的应力增量σ
作用下叠合构件纵向受拉钢筋的应力增量σ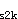 可按下式计算:
可按下式计算:
σ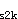 =
= =152.3N/mm
=152.3N/mm
最后得到叠合构件纵向受拉钢筋的应力为:
σ =σ
=σ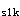 +σ
+σ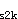 =133.9+152.3=286.2N/mm
=133.9+152.3=286.2N/mm <0.9f
<0.9f =0.9×360=324N/mm
=0.9×360=324N/mm
所以选项D是正确的。选项A是错误地取用了σ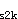 =M
=M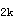 /0.87h
/0.87h A
A 所得结果;选项B与C都是计算错误。
所得结果;选项B与C都是计算错误。
M
 =1/8(q
=1/8(q ι
ι )=(1/8)×12×6
)=(1/8)×12×6 =54kN·m
=54kN·mM
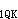 =1/8(q
=1/8(q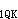 ι
ι )=(1/8)×6×6
)=(1/8)×6×6 =27kN·m
=27kN·m(2)第二阶段:叠合层混凝土达到设计规定的强度后,叠合构件应按整体结构计算。对跨中截面:
M
 =0.6×(1/8)×10×6
=0.6×(1/8)×10×6 =27kN·m
=27kN·mM
 =0.6×(1/8)×24×6
=0.6×(1/8)×24×6 =64.8kN·m
=64.8kN·m于是在正弯矩区段,根据《混凝土结构设计规范》10.6.3条有:
M=1.2M
 +1.2M
+1.2M +1.4M
+1.4M =1.2×54+1.2×27+1.4×64.8=187.92kN·m
=1.2×54+1.2×27+1.4×64.8=187.92kN·m在负弯矩区段,对支座截面:
M
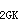 =(1-0.6)×(1/8)×10×6
=(1-0.6)×(1/8)×10×6 =18kN·m
=18kN·mM
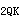 =(1-0.6)×(1/8)×24×6
=(1-0.6)×(1/8)×24×6 =43.2kN·m
=43.2kN·mM=1.2M
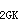 +1.4M
+1.4M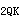 =1.2×18+1.4×43.2=82.08kN·m
=1.2×18+1.4×43.2=82.08kN·m因此选项C是正确的。
选项B的错误在于对跨中截面及支座截面均取:M
 =(1/8)×10×6
=(1/8)×10×6 =45kN·m
=45kN·mM
 =(1/8)×24×6
=(1/8)×24×6 =108kN·m这就得到:对跨中截面M=1.2×54+1.2×45+1.4×108=270kN·m
=108kN·m这就得到:对跨中截面M=1.2×54+1.2×45+1.4×108=270kN·m对支座截面M=1.2×45+1.4×108=205kN·m
选项A的错误在于在选项B的基础上,将第一阶段施工活荷载产生的弯矩值亦加上。
选项D则是未考虑叠合构件的特点,按照整体结构计算所得结果。即:
对跨中截面M=1.2×0.6×(1/8)×(12+10)×6
 +1.4×0.6×(1/8)×24×6
+1.4×0.6×(1/8)×24×6 =162kN·m
=162kN·m对支座截面M=1.2×0.4×(1/8)×(12+10)×6
 +1.4×0.4×(1/8)×24×6
+1.4×0.4×(1/8)×24×6 =108kN·m
=108kN·m所以选项A、B、D都是不正确的。
【点评】:(1)叠合梁在20世纪60~70年代,为了节约木材,曾于我国工业与民用建筑工程中得到广泛的应用,也做了大量的试验研究工作。经验表明,当h
 /h<0.4时,应在施工阶段设置可靠的支撑,且h
/h<0.4时,应在施工阶段设置可靠的支撑,且h /h<0.4的二阶段受力叠合构件,其受力性能和经济效果均较差,裂缝及挠度很难满足使用要求。
/h<0.4的二阶段受力叠合构件,其受力性能和经济效果均较差,裂缝及挠度很难满足使用要求。(2)试验表明,叠合构件的受弯承载力约有25%的试件达不到整体构件的受弯承载力,曾有专家建议将规范公式(10.6.3-2)改为:
正弯矩区段M=[1.7-0.7(h
 /h)]M
/h)]M +M
+M +M
+M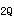
因此提请结构工程师注意,在设计叠合构件时正截面受弯承载力留有适当余地为好。
(3)规范10.6.3条对叠合构件的弯矩设计值作了如下规定:
正弯矩区段M=M
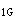 +M
+M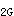 +M
+M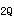
负弯矩区段M=M
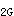 +M
+M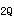
式中M
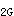 --第二阶段面层、吊顶等自重在计算截面产生的弯矩设计值;
--第二阶段面层、吊顶等自重在计算截面产生的弯矩设计值;M
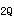 --第二阶段可变荷载在计算截面产生的弯矩设计值。
--第二阶段可变荷载在计算截面产生的弯矩设计值。M
 、M
、M 均应按整体结构计算,且跨中截面和支座截面一般为不同的数值。由于在正弯矩区段和负弯矩区段均采用同一符号表示,于是有些结构工程师便错误地理解为应取同一数值,这是不正确的,例如本题选项B便是如此。
均应按整体结构计算,且跨中截面和支座截面一般为不同的数值。由于在正弯矩区段和负弯矩区段均采用同一符号表示,于是有些结构工程师便错误地理解为应取同一数值,这是不正确的,例如本题选项B便是如此。第1小题:【主要解答过程如下】:(1)A
 =1256mm
=1256mm (4
(4 20),根据《混凝土结构设计规范》式(10.6.8-3),在弯矩M
20),根据《混凝土结构设计规范》式(10.6.8-3),在弯矩M 作用下,预制构件纵向受拉钢筋的应力为:
作用下,预制构件纵向受拉钢筋的应力为:σ
 =M
=M /0.87A
/0.87A h
h =60×10
=60×10 /0.87×1256×(450-40)=133.9N/mm
/0.87×1256×(450-40)=133.9N/mm
下面按T形截面计算预制构件的正截面受弯承载力设计值M
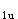 。
。依据规范7.2.2条,f
 A
A =360×1256=452160N<α
=360×1256=452160N<α f
f b′
b′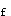 h′
h′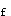 =1.0×14.3×500×120
=1.0×14.3×500×120故应按宽度为500mm的矩形截面计算。
按规范7.2.1条,α
 f
f b′
b′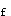 x=1.0×14.3×500x=f
x=1.0×14.3×500x=f A
A =360×1256=452160
=360×1256=452160x=452160/1.0×14.3×500=63.24mm
M
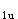 =α
=α f
f b′
b′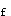 x=1.0×14.3×500×63.24×[410-(1/2)×63.24]=171.09×10
x=1.0×14.3×500×63.24×[410-(1/2)×63.24]=171.09×10 N·mm
N·mmM
 =60kN·m>0.35M
=60kN·m>0.35M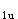 =0.35×171.09=59.88kN·m
=0.35×171.09=59.88kN·m于是从10.6.8条,在弯矩M
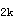 作用下叠合构件纵向受拉钢筋的应力增量σ
作用下叠合构件纵向受拉钢筋的应力增量σ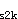 可按下式计算:
可按下式计算:σ
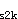 =
= =152.3N/mm
=152.3N/mm
最后得到叠合构件纵向受拉钢筋的应力为:
σ
 =σ
=σ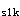 +σ
+σ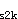 =133.9+152.3=286.2N/mm
=133.9+152.3=286.2N/mm <0.9f
<0.9f =0.9×360=324N/mm
=0.9×360=324N/mm
所以选项D是正确的。选项A是错误地取用了σ
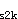 =M
=M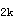 /0.87h
/0.87h A
A 所得结果;选项B与C都是计算错误。
所得结果;选项B与C都是计算错误。