某五层钢筋混凝土框架结构,房屋高度24m,丙类建筑,抗震设防烈度为9度,建筑场地为工类;其结构平面布置见图1-10-1,板厚110mm,第二层楼面框架梁KL-4的截面尺寸为400mm×900mm,中柱柱截面尺寸为900mm×900mm,边柱柱截面尺寸为700mm×700mm(图2-10-1);混凝土强度等级C30,纵向钢筋采用HRB400级钢筋,箍筋采用HRB335级钢筋。现对其轴线 -
- 梁段进行设计。
梁段进行设计。
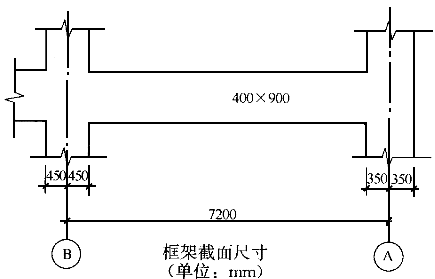
 -
-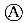 梁段进行设计。
梁段进行设计。
- 现已计算出支座
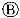 柱边缘处的负弯矩设计值为1715kN·m,上部钢筋采用二排布置,h
柱边缘处的负弯矩设计值为1715kN·m,上部钢筋采用二排布置,h =820mm;下部钢筋采用一排布置,由跨中钢筋直通入支座的钢筋为5
=820mm;下部钢筋采用一排布置,由跨中钢筋直通入支座的钢筋为5 28,h
28,h =855mm,问上部钢筋及相对受压区高度x/h
=855mm,问上部钢筋及相对受压区高度x/h 。值与下列哪项最接近?A.4
。值与下列哪项最接近?A.4 28+5
28+5 25,x/h
25,x/h =0.118<0.25B.6
=0.118<0.25B.6 32,x/h
32,x/h =0.134<0.35C.9
=0.134<0.35C.9 28,x/h
28,x/h =0.19<0.25D.9
=0.19<0.25D.9 28,x/h
28,x/h =0.19<0.35
=0.19<0.35 - 框架梁在
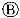 支座及
支座及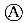 支座处的配筋如图2-11-1所示。
支座处的配筋如图2-11-1所示。

经计算机内力分析,并按一级抗震等级对上述内力进行调整后,考虑地震作用组合的梁⑧端支座边缘由梁端弯矩产生的剪力设计值为514kN;梁在重力荷载代表值作用下按简支梁计算时,其荷载简图见2-11-2,图中6400mm为柱边缘之间的距离。
集中荷载标准值p =219.52kN
=219.52kN
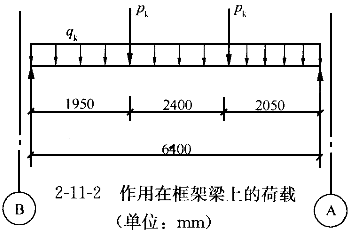
均布荷载标准值q =9kN/m
=9kN/m
梁上部钢筋的a =80mm,下部钢筋的a′
=80mm,下部钢筋的a′ =45mm,并假定由集中荷载产生的剪力(含地震作用产生的剪力)与总剪力计算值之比大于0.75。问加密区的箍筋配置及非加密区的箍筋配置,采用下列哪一组最适宜?A.4
=45mm,并假定由集中荷载产生的剪力(含地震作用产生的剪力)与总剪力计算值之比大于0.75。问加密区的箍筋配置及非加密区的箍筋配置,采用下列哪一组最适宜?A.4 8@100、4
8@100、4 8@200B.4
8@200B.4 10@100、4
10@100、4 10@200C.4
10@200C.4 10@100、4
10@100、4 10@170D.4
10@170D.4 8@100、4
8@100、4 8@150
8@150
正确答案:
(1)B
(2)C
(2)C
答案解析:
第1小题:【主要解答过程如下】:根据《混凝土结构设计规范》7.2.1条及11.3.1条,梁配筋应按下列公式计算:
γ M≤α
M≤α f
f bx(h
bx(h -x/2)+f′
-x/2)+f′ A′
A′ (h
(h -a′
-a′ )(2-10-1)
)(2-10-1)
α f
f bx=f
bx=f A
A -f′
-f′ A′
A′ (2-10-2)
(2-10-2)
式中γ =0.75(按规范表11.1.6)
=0.75(按规范表11.1.6)
已知A′ =3079mm
=3079mm (5
(5 28)
28)
α f
f bx=360(A
bx=360(A -A′
-A′ )=360(A
)=360(A -3079)
-3079)
x=360(A -3079)/1.0×400×14.3=0.06294A
-3079)/1.0×400×14.3=0.06294A -193.78
-193.78
将x代入式(2-10-1)得:0.75×1715×10 =360(A
=360(A -3079)×[820-(0.06294A
-3079)×[820-(0.06294A -193.78)/2]+360×3079×(820-45)
-193.78)/2]+360×3079×(820-45)
化简以后得到:A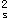 -32214A
-32214A +127416459=0
+127416459=0
A =4617mm
=4617mm
x=0.06294×4617-193.78=96.8mm>2a′ =90mm(可)
=90mm(可)
选用6 32(A
32(A =4826mm
=4826mm )
)
根据《建筑抗震设计规范》表6.1.2,此房屋的抗震等级为一级,但又从该规范3.3.2条,当建筑场地为Ⅰ类时,允许按8度采取抗震构造措施,于是查表6.1.2得知,框架结构可按二级采取抗震构造措施。
依据《混凝土结构设计规范》11.3.1条,计入纵向受压钢筋的梁端混凝土受压区高度,对二级抗震等级应符合x≤0.35h 的要求,且梁端纵向受拉钢筋的配筋率不应大于2.5%。
的要求,且梁端纵向受拉钢筋的配筋率不应大于2.5%。
ρ=A /bh
/bh =4826/400×820=1.47%<2.5%(可)
=4826/400×820=1.47%<2.5%(可)
当计算x时应采用实配钢筋面积,不应采用计算钢筋面积。由此得到:
x=360(A -A′
-A′ )/α
)/α f
f b=360(4826-3079)/1.0×14.3×400=110mm
b=360(4826-3079)/1.0×14.3×400=110mm
ζ=x/h =110/820=0.134<0.35(符合对二级抗震等级框架梁的构造要求)。
=110/820=0.134<0.35(符合对二级抗震等级框架梁的构造要求)。
所以选项B是正确的。A的错误在于以一级抗震等级的要求x/h ≤0.25为衡量标准,且计算受压区高度时以计算面积为准;C和D均未考虑受压钢筋的作用。
≤0.25为衡量标准,且计算受压区高度时以计算面积为准;C和D均未考虑受压钢筋的作用。
【点评】:框架梁的抗震构造设计,要求梁端计入受压钢筋的受压区高度和有效高度之比x/h ,当抗震等级为一级时不应大于0.25,二、三级时不应大于0.35,这是框架梁延性设计的要求。在强烈地震作用下,如果设计得当,结构梁端必定要出现塑性铰,在塑性铰区域内,全部实配钢筋均将屈服,而不会只是计算配筋量;且x/h
,当抗震等级为一级时不应大于0.25,二、三级时不应大于0.35,这是框架梁延性设计的要求。在强烈地震作用下,如果设计得当,结构梁端必定要出现塑性铰,在塑性铰区域内,全部实配钢筋均将屈服,而不会只是计算配筋量;且x/h 愈小,则根据平截面假定受拉钢筋进入屈服后的拉应变愈大,也就是延性愈好。
愈小,则根据平截面假定受拉钢筋进入屈服后的拉应变愈大,也就是延性愈好。
第2小题:【主要解答过程如下】:(1)根据《混凝土结构设计规范》11.3.2条的条文说明,M =(1/γ
=(1/γ )f
)f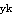 A
A (h
(h -a′
-a′ )
)
梁上部配筋A =4599mm
=4599mm (5
(5 28,4
28,4 22)
22)
梁下部配筋A =3079mm
=3079mm (5
(5 28)
28)
左端M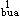 =(1/0.75)×400×4599×(900-80-45)=190092×10
=(1/0.75)×400×4599×(900-80-45)=190092×10 N·mm=1900.92kN·m
N·mm=1900.92kN·m
右端M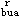 =(1/0.75)×400×3079×(900-80-45)=122370×10
=(1/0.75)×400×3079×(900-80-45)=122370×10 N·mm=1223.7kN·m
N·mm=1223.7kN·m
按规范11.3.2条,对一级抗震等级的框架结构:1.1(M +M
+M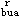 )/ln=1.1×(1900.92+1223.7)/6.4=537.05kN>514kN
)/ln=1.1×(1900.92+1223.7)/6.4=537.05kN>514kN
因此,梁端的剪力设计值由实配钢筋控制。又从图2-11-2可得:
V =1.2×[(1/2)×6.4×9+219.52×(2.05+4.45)/6.4]=302.1kN
=1.2×[(1/2)×6.4×9+219.52×(2.05+4.45)/6.4]=302.1kN
最后得到V =537.05+302.1=839.15kN
=537.05+302.1=839.15kN
(2)验算截面控制条件
根据规范11.3.3条,当跨高比大于2.5时,受剪截面应符合下列条件:
V ≤(1/γ
≤(1/γ )(0.2β
)(0.2β f
f bh
bh )
)
(1/γ )(0.2β
)(0.2β f
f bh
bh )=(1/0.85)×0.2×1.0×14.3×400×820=1103623N=1103.623kN>839.15kN(符合要求)
)=(1/0.85)×0.2×1.0×14.3×400×820=1103623N=1103.623kN>839.15kN(符合要求)
(3)加密区受剪承载力计算
从规范11.3.4条,斜截面受剪承载力应按下式计算:
V =
=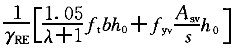 (2-11-1)
(2-11-1)
剪距比λ=a/h =1.95/0.82=2.378
=1.95/0.82=2.378
故B39150=1/0.85×1.43×400×820+300×(A[http://cdn.laixue.com/exam/20405168/TestImages/sv.gif) /S)×820]
/S)×820]
A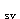 /S=2.307mm
/S=2.307mm
又由11.3.6条,对二级抗震等级取加密区箍筋间距S=100mm,同时箍筋最小直径为8mm。
A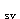 =2.307×100=230.7mm
=2.307×100=230.7mm
选用 10@100四肢箍,A
10@100四肢箍,A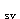 =4×78.5=314mm
=4×78.5=314mm >230.7mm
>230.7mm
对抗震等级为二级的框架梁,加密区箍筋肢距<250mm(符合规范11.3.8条的构造要求)。
箍筋加密区长度为1.5h,等于1350mm。
(4)非箍筋加密区受剪承载力计算
应取箍筋加密区末端处的剪力计算,且计算时无需对剪力进行调整。
V=514/1.3+302.1-1.2×9×1.35=682.9kN
注:式中1.30为一级抗震等级的内力调整系数,见规范11.3.2条。
将上述数据代入式(2-11-1)得:
γ
 M≤α
M≤α f
f bx(h
bx(h -x/2)+f′
-x/2)+f′ A′
A′ (h
(h -a′
-a′ )(2-10-1)
)(2-10-1)α
 f
f bx=f
bx=f A
A -f′
-f′ A′
A′ (2-10-2)
(2-10-2)式中γ
 =0.75(按规范表11.1.6)
=0.75(按规范表11.1.6)已知A′
 =3079mm
=3079mm (5
(5 28)
28)α
 f
f bx=360(A
bx=360(A -A′
-A′ )=360(A
)=360(A -3079)
-3079)x=360(A
 -3079)/1.0×400×14.3=0.06294A
-3079)/1.0×400×14.3=0.06294A -193.78
-193.78将x代入式(2-10-1)得:0.75×1715×10
 =360(A
=360(A -3079)×[820-(0.06294A
-3079)×[820-(0.06294A -193.78)/2]+360×3079×(820-45)
-193.78)/2]+360×3079×(820-45)化简以后得到:A
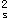 -32214A
-32214A +127416459=0
+127416459=0A
 =4617mm
=4617mm
x=0.06294×4617-193.78=96.8mm>2a′
 =90mm(可)
=90mm(可)选用6
 32(A
32(A =4826mm
=4826mm )
)根据《建筑抗震设计规范》表6.1.2,此房屋的抗震等级为一级,但又从该规范3.3.2条,当建筑场地为Ⅰ类时,允许按8度采取抗震构造措施,于是查表6.1.2得知,框架结构可按二级采取抗震构造措施。
依据《混凝土结构设计规范》11.3.1条,计入纵向受压钢筋的梁端混凝土受压区高度,对二级抗震等级应符合x≤0.35h
 的要求,且梁端纵向受拉钢筋的配筋率不应大于2.5%。
的要求,且梁端纵向受拉钢筋的配筋率不应大于2.5%。ρ=A
 /bh
/bh =4826/400×820=1.47%<2.5%(可)
=4826/400×820=1.47%<2.5%(可)当计算x时应采用实配钢筋面积,不应采用计算钢筋面积。由此得到:
x=360(A
 -A′
-A′ )/α
)/α f
f b=360(4826-3079)/1.0×14.3×400=110mm
b=360(4826-3079)/1.0×14.3×400=110mmζ=x/h
 =110/820=0.134<0.35(符合对二级抗震等级框架梁的构造要求)。
=110/820=0.134<0.35(符合对二级抗震等级框架梁的构造要求)。所以选项B是正确的。A的错误在于以一级抗震等级的要求x/h
 ≤0.25为衡量标准,且计算受压区高度时以计算面积为准;C和D均未考虑受压钢筋的作用。
≤0.25为衡量标准,且计算受压区高度时以计算面积为准;C和D均未考虑受压钢筋的作用。【点评】:框架梁的抗震构造设计,要求梁端计入受压钢筋的受压区高度和有效高度之比x/h
 ,当抗震等级为一级时不应大于0.25,二、三级时不应大于0.35,这是框架梁延性设计的要求。在强烈地震作用下,如果设计得当,结构梁端必定要出现塑性铰,在塑性铰区域内,全部实配钢筋均将屈服,而不会只是计算配筋量;且x/h
,当抗震等级为一级时不应大于0.25,二、三级时不应大于0.35,这是框架梁延性设计的要求。在强烈地震作用下,如果设计得当,结构梁端必定要出现塑性铰,在塑性铰区域内,全部实配钢筋均将屈服,而不会只是计算配筋量;且x/h 愈小,则根据平截面假定受拉钢筋进入屈服后的拉应变愈大,也就是延性愈好。
愈小,则根据平截面假定受拉钢筋进入屈服后的拉应变愈大,也就是延性愈好。第2小题:【主要解答过程如下】:(1)根据《混凝土结构设计规范》11.3.2条的条文说明,M
 =(1/γ
=(1/γ )f
)f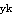 A
A (h
(h -a′
-a′ )
)梁上部配筋A
 =4599mm
=4599mm (5
(5 28,4
28,4 22)
22)梁下部配筋A
 =3079mm
=3079mm (5
(5 28)
28)左端M
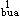 =(1/0.75)×400×4599×(900-80-45)=190092×10
=(1/0.75)×400×4599×(900-80-45)=190092×10 N·mm=1900.92kN·m
N·mm=1900.92kN·m右端M
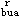 =(1/0.75)×400×3079×(900-80-45)=122370×10
=(1/0.75)×400×3079×(900-80-45)=122370×10 N·mm=1223.7kN·m
N·mm=1223.7kN·m按规范11.3.2条,对一级抗震等级的框架结构:1.1(M
 +M
+M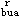 )/ln=1.1×(1900.92+1223.7)/6.4=537.05kN>514kN
)/ln=1.1×(1900.92+1223.7)/6.4=537.05kN>514kN因此,梁端的剪力设计值由实配钢筋控制。又从图2-11-2可得:
V
 =1.2×[(1/2)×6.4×9+219.52×(2.05+4.45)/6.4]=302.1kN
=1.2×[(1/2)×6.4×9+219.52×(2.05+4.45)/6.4]=302.1kN最后得到V
 =537.05+302.1=839.15kN
=537.05+302.1=839.15kN(2)验算截面控制条件
根据规范11.3.3条,当跨高比大于2.5时,受剪截面应符合下列条件:
V
 ≤(1/γ
≤(1/γ )(0.2β
)(0.2β f
f bh
bh )
)(1/γ
 )(0.2β
)(0.2β f
f bh
bh )=(1/0.85)×0.2×1.0×14.3×400×820=1103623N=1103.623kN>839.15kN(符合要求)
)=(1/0.85)×0.2×1.0×14.3×400×820=1103623N=1103.623kN>839.15kN(符合要求)(3)加密区受剪承载力计算
从规范11.3.4条,斜截面受剪承载力应按下式计算:
V
 =
=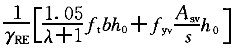 (2-11-1)
(2-11-1)剪距比λ=a/h
 =1.95/0.82=2.378
=1.95/0.82=2.378故B39150=1/0.85
×1.43×400×820+300×(A[http://cdn.laixue.com/exam/20405168/TestImages/sv.gif) /S)×820]
/S)×820]A
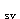 /S=2.307mm
/S=2.307mm又由11.3.6条,对二级抗震等级取加密区箍筋间距S=100mm,同时箍筋最小直径为8mm。
A
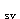 =2.307×100=230.7mm
=2.307×100=230.7mm
选用
 10@100四肢箍,A
10@100四肢箍,A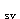 =4×78.5=314mm
=4×78.5=314mm >230.7mm
>230.7mm
对抗震等级为二级的框架梁,加密区箍筋肢距<250mm(符合规范11.3.8条的构造要求)。
箍筋加密区长度为1.5h,等于1350mm。
(4)非箍筋加密区受剪承载力计算
应取箍筋加密区末端处的剪力计算,且计算时无需对剪力进行调整。
V=514/1.3+302.1-1.2×9×1.35=682.9kN
注:式中1.30为一级抗震等级的内力调整系数,见规范11.3.2条。
将上述数据代入式(2-11-1)得:
