某框架-核心筒结构,框架主梁左端与框架柱刚接,右端与核心筒铰结,跨度8m,截面尺寸为500mm×600mm;混凝土强度等级C35,采用HRB335级钢筋;其支座及跨中截面配筋见图2-12-1;非抗震设计,γ =1.1;经计算在竖向荷载作用下,跨中截面的正弯矩标准值为M
=1.1;经计算在竖向荷载作用下,跨中截面的正弯矩标准值为M =309.6kN·m,轴线①支座截面的负弯矩标准值为M
=309.6kN·m,轴线①支座截面的负弯矩标准值为M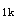 =-337.5kN·m,跨中截面按永久荷载和活荷载效应的准永久组合弯矩值为M
=-337.5kN·m,跨中截面按永久荷载和活荷载效应的准永久组合弯矩值为M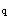 =276.4kN·m,轴线①支座截面按永久荷载和活荷载效应的准永久组合的负弯矩值为M
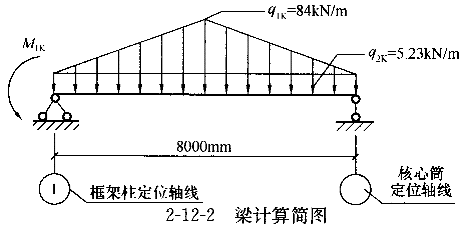
=276.4kN·m,轴线①支座截面按永久荷载和活荷载效应的准永久组合的负弯矩值为M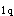 =329.5kN·m;在荷载标准值作用下框架梁的计算简图见图2-12-2。
=329.5kN·m;在荷载标准值作用下框架梁的计算简图见图2-12-2。
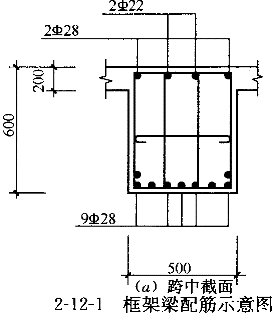
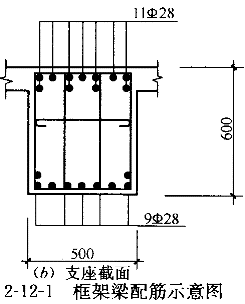
若梁不考虑楼板作用按矩形截面计算,且跨中截面h =540mm,支座截面h
=540mm,支座截面h =530mm,则梁跨中最大挠度与下列哪一个数值最接近?(提示:在支座负弯矩作用下,梁跨中挠度最大值可按f=0.0624Mι
=530mm,则梁跨中最大挠度与下列哪一个数值最接近?(提示:在支座负弯矩作用下,梁跨中挠度最大值可按f=0.0624Mι /EI计算;在三角形荷载作用下,梁跨中挠度按f=qι
/EI计算;在三角形荷载作用下,梁跨中挠度按f=qι /120EI计算。)
/120EI计算。)
 =1.1;经计算在竖向荷载作用下,跨中截面的正弯矩标准值为M
=1.1;经计算在竖向荷载作用下,跨中截面的正弯矩标准值为M =309.6kN·m,轴线①支座截面的负弯矩标准值为M
=309.6kN·m,轴线①支座截面的负弯矩标准值为M =-337.5kN·m,跨中截面按永久荷载和活荷载效应的准永久组合弯矩值为M
=-337.5kN·m,跨中截面按永久荷载和活荷载效应的准永久组合弯矩值为M =276.4kN·m,轴线①支座截面按永久荷载和活荷载效应的准永久组合的负弯矩值为M
=276.4kN·m,轴线①支座截面按永久荷载和活荷载效应的准永久组合的负弯矩值为M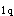 =329.5kN·m;在荷载标准值作用下框架梁的计算简图见图2-12-2。
=329.5kN·m;在荷载标准值作用下框架梁的计算简图见图2-12-2。


若梁不考虑楼板作用按矩形截面计算,且跨中截面h
 =540mm,支座截面h
=540mm,支座截面h =530mm,则梁跨中最大挠度与下列哪一个数值最接近?(提示:在支座负弯矩作用下,梁跨中挠度最大值可按f=0.0624Mι
=530mm,则梁跨中最大挠度与下列哪一个数值最接近?(提示:在支座负弯矩作用下,梁跨中挠度最大值可按f=0.0624Mι /EI计算;在三角形荷载作用下,梁跨中挠度按f=qι
/EI计算;在三角形荷载作用下,梁跨中挠度按f=qι /120EI计算。)
/120EI计算。) 正确答案:
D
答案解析:
【主要解答过程如下】:(1)梁跨中截面的刚度计算
根据《混凝土结构设计规范》公式(8.2.3-1),受弯构件跨中截面的短期刚度为:
B =E
=E A
A h
h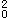 /1.15ψ+0.2+(6α
/1.15ψ+0.2+(6α ρ/1+3.5γ′
ρ/1+3.5γ′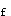 )
)
式中A =5542mm
=5542mm (9
(9 28)
28)
从公式(8.1.3-3),σ =M
=M /0.87h
/0.87h A
A =309.6×10
=309.6×10 /0.87×540×5542=118.9N/mm
/0.87×540×5542=118.9N/mm
又从规范8.1.2条,A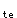 =0.5bh=0.5×500×600=150000mm
=0.5bh=0.5×500×600=150000mm
ρ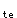 =A
=A /A
/A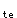 =5542/150000=0.0369
=5542/150000=0.0369
ψ=1.1-0.65(f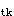 /ρ
/ρ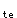 σ
σ )=1.1-0.65×(2.2/0.0369×118.9)=0.774
)=1.1-0.65×(2.2/0.0369×118.9)=0.774
α =E
=E /E
/E =2.0×10
=2.0×10 /3.15×10
/3.15×10 =6.349
=6.349
A′ =1992mm
=1992mm (2
(2 28,2
28,2 22)
22)
ρ=A /bh
/bh =5542/500×540=0.0205
=5542/500×540=0.0205
ρ′=A′ /bh
/bh =1992/500×540=0.00738=0.369
=1992/500×540=0.00738=0.369
因按矩形截面计算γ′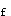 =0。
=0。
梁跨中截面的短期刚度为:
B =2.0×10
=2.0×10 ×5542×540
×5542×540 /1.15×0.774+0.2+6×6.349×0.0205=1.727×10
/1.15×0.774+0.2+6×6.349×0.0205=1.727×10 N·mm
N·mm
按规范8.2.5条,θ=2-0.4×0.36=1.856
依据规范公式(8.2.2),矩形截面梁跨中截面的长期刚度为:
B=[M /M
/M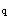 (θ-1)+M
(θ-1)+M ]B
]B =[309.6×10
=[309.6×10 /276.4×10
/276.4×10 (1.856-1)+309.6×10
(1.856-1)+309.6×10 ]×1.727×10
]×1.727×10
=9.79×10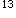 N·mm
N·mm
(2)梁①轴支座截面刚度计算
A =6774mm
=6774mm (11
(11 28),A′
28),A′ =5542mm
=5542mm (9
(9 28)
28)
σ =M
=M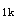 /0.87h
/0.87h A
A =337.5×10[~6.gif/0.87×530×6774]=108N/mm
=337.5×10[~6.gif/0.87×530×6774]=108N/mm ρ
ρ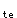 =A
=A /A
/A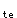 =6774/150000=0.04516ψ=1-0.65(f
=6774/150000=0.04516ψ=1-0.65(f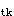 /ρ
/ρ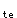 σ
σ )=1-(2.2/0.04516×108)=0.807ρ=A
)=1-(2.2/0.04516×108)=0.807ρ=A /bh
/bh =6774/500×530=0.0256ρ′=A′
=6774/500×530=0.0256ρ′=A′ /bh
/bh =5542/500×530=0.0209=0.8169
=5542/500×530=0.0209=0.8169
所以梁①轴支座截面的短期刚度为:
B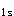 =2.0×10
=2.0×10 ×6774×530
×6774×530 /1.15×0.807+0.2+6×6.349×0.0256=1.81×10
/1.15×0.807+0.2+6×6.349×0.0256=1.81×10 N·mm
N·mm
θ=2-0.4×0.816=1.674
矩形截面梁①轴支座截面的长期刚度为:
B =[M
=[M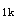 /M
/M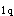 (θ-1)+M
(θ-1)+M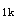 ]B
]B =[337.5/329.5(1.674-1)+337.5]×1.81×10
=[337.5/329.5(1.674-1)+337.5]×1.81×10 =1.092×10
=1.092×10 N·mm
N·mm
B /B=10.92/9.79=1.11,2>1.11>0.5
/B=10.92/9.79=1.11,2>1.11>0.5
故按规范8.2.1条,框架梁可按等刚度受弯构件进行挠度计算,其刚度可取梁跨中最大弯矩截面的刚度,即B=9.79×10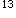 N·mm
N·mm 。
。
(3)梁跨中挠度计算
梁跨中挠度计算简图见图2-12-2。于是在荷载效应的标准组合并考虑荷载长期作用影响下梁的跨中挠度近似值为:
f=5q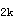 ι
ι /384B+q
/384B+q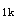 ι
ι /120B-0.0624(M
/120B-0.0624(M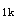 ι
ι /B)
/B)
=5×5.23×8000 /384×9.79×10
/384×9.79×10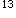 +84×8000
+84×8000 /120×9.79×10
/120×9.79×10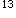 -0.0624384×(337.5×10
-0.0624384×(337.5×10 ×8000
×8000 /9.9×10
/9.9×10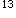 )
)
=2.85+29.29-14.15=18mm
此即选项D。选项A是错误地取用了短期刚度计算所得结果;选项B采用了长期刚度计算,但错误地乘以重要性系数γ =1.10,重要性系数仅用于承载能力计算,不应用于正常使用极限状态验算;选项C则采用了短期刚度计算,并乘以重要性系数1.10;因此均是不正确的。
=1.10,重要性系数仅用于承载能力计算,不应用于正常使用极限状态验算;选项C则采用了短期刚度计算,并乘以重要性系数1.10;因此均是不正确的。
【点评】:(1)本题是挠度计算的基本方法,考生应当熟练掌握。
(2)本题计算时按规定忽略了楼板(翼缘)的作用;使得梁的刚度减小较多,也使计算得出的梁挠度偏大。
(3)框架梁的配筋系根据抗震设防烈度为8度时的计算结果配置,因此配筋较多,这对按正常使用极限状态对构件进行验算有利。
(4)规范8.2.1条中挠度计算时对构件刚度取值的规定系根据等截面构件计算比较得到,但符合刚度比条件的变截面梁也适用,请考生注意。
根据《混凝土结构设计规范》公式(8.2.3-1),受弯构件跨中截面的短期刚度为:
B
 =E
=E A
A h
h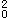 /1.15ψ+0.2+(6α
/1.15ψ+0.2+(6α ρ/1+3.5γ′
ρ/1+3.5γ′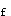 )
)式中A
 =5542mm
=5542mm (9
(9 28)
28)从公式(8.1.3-3),σ
 =M
=M /0.87h
/0.87h A
A =309.6×10
=309.6×10 /0.87×540×5542=118.9N/mm
/0.87×540×5542=118.9N/mm
又从规范8.1.2条,A
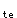 =0.5bh=0.5×500×600=150000mm
=0.5bh=0.5×500×600=150000mm
ρ
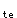 =A
=A /A
/A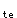 =5542/150000=0.0369
=5542/150000=0.0369ψ=1.1-0.65(f
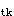 /ρ
/ρ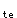 σ
σ )=1.1-0.65×(2.2/0.0369×118.9)=0.774
)=1.1-0.65×(2.2/0.0369×118.9)=0.774α
 =E
=E /E
/E =2.0×10
=2.0×10 /3.15×10
/3.15×10 =6.349
=6.349A′
 =1992mm
=1992mm (2
(2 28,2
28,2 22)
22)ρ=A
 /bh
/bh =5542/500×540=0.0205
=5542/500×540=0.0205ρ′=A′
 /bh
/bh =1992/500×540=0.00738=0.369
=1992/500×540=0.00738=0.369因按矩形截面计算γ′
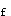 =0。
=0。梁跨中截面的短期刚度为:
B
 =2.0×10
=2.0×10 ×5542×540
×5542×540 /1.15×0.774+0.2+6×6.349×0.0205=1.727×10
/1.15×0.774+0.2+6×6.349×0.0205=1.727×10 N·mm
N·mm
按规范8.2.5条,θ=2-0.4×0.36=1.856
依据规范公式(8.2.2),矩形截面梁跨中截面的长期刚度为:
B=[M
 /M
/M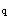 (θ-1)+M
(θ-1)+M ]B
]B =[309.6×10
=[309.6×10 /276.4×10
/276.4×10 (1.856-1)+309.6×10
(1.856-1)+309.6×10 ]×1.727×10
]×1.727×10
=9.79×10
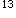 N·mm
N·mm
(2)梁①轴支座截面刚度计算
A
 =6774mm
=6774mm (11
(11 28),A′
28),A′ =5542mm
=5542mm (9
(9 28)
28)σ
 =M
=M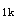 /0.87h
/0.87h A
A =337.5×10[~6.gif/0.87×530×6774]=108N/mm
=337.5×10[~6.gif/0.87×530×6774]=108N/mm ρ
ρ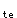 =A
=A /A
/A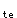 =6774/150000=0.04516ψ=1-0.65(f
=6774/150000=0.04516ψ=1-0.65(f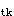 /ρ
/ρ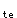 σ
σ )=1-(2.2/0.04516×108)=0.807ρ=A
)=1-(2.2/0.04516×108)=0.807ρ=A /bh
/bh =6774/500×530=0.0256ρ′=A′
=6774/500×530=0.0256ρ′=A′ /bh
/bh =5542/500×530=0.0209=0.8169
=5542/500×530=0.0209=0.8169所以梁①轴支座截面的短期刚度为:
B
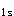 =2.0×10
=2.0×10 ×6774×530
×6774×530 /1.15×0.807+0.2+6×6.349×0.0256=1.81×10
/1.15×0.807+0.2+6×6.349×0.0256=1.81×10 N·mm
N·mm
θ=2-0.4×0.816=1.674
矩形截面梁①轴支座截面的长期刚度为:
B
 =[M
=[M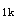 /M
/M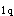 (θ-1)+M
(θ-1)+M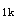 ]B
]B =[337.5/329.5(1.674-1)+337.5]×1.81×10
=[337.5/329.5(1.674-1)+337.5]×1.81×10 =1.092×10
=1.092×10 N·mm
N·mm
B
 /B=10.92/9.79=1.11,2>1.11>0.5
/B=10.92/9.79=1.11,2>1.11>0.5故按规范8.2.1条,框架梁可按等刚度受弯构件进行挠度计算,其刚度可取梁跨中最大弯矩截面的刚度,即B=9.79×10
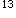 N·mm
N·mm 。
。(3)梁跨中挠度计算
梁跨中挠度计算简图见图2-12-2。于是在荷载效应的标准组合并考虑荷载长期作用影响下梁的跨中挠度近似值为:
f=5q
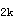 ι
ι /384B+q
/384B+q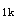 ι
ι /120B-0.0624(M
/120B-0.0624(M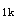 ι
ι /B)
/B)=5×5.23×8000
 /384×9.79×10
/384×9.79×10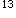 +84×8000
+84×8000 /120×9.79×10
/120×9.79×10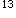 -0.0624384×(337.5×10
-0.0624384×(337.5×10 ×8000
×8000 /9.9×10
/9.9×10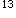 )
)=2.85+29.29-14.15=18mm
此即选项D。选项A是错误地取用了短期刚度计算所得结果;选项B采用了长期刚度计算,但错误地乘以重要性系数γ
 =1.10,重要性系数仅用于承载能力计算,不应用于正常使用极限状态验算;选项C则采用了短期刚度计算,并乘以重要性系数1.10;因此均是不正确的。
=1.10,重要性系数仅用于承载能力计算,不应用于正常使用极限状态验算;选项C则采用了短期刚度计算,并乘以重要性系数1.10;因此均是不正确的。【点评】:(1)本题是挠度计算的基本方法,考生应当熟练掌握。
(2)本题计算时按规定忽略了楼板(翼缘)的作用;使得梁的刚度减小较多,也使计算得出的梁挠度偏大。
(3)框架梁的配筋系根据抗震设防烈度为8度时的计算结果配置,因此配筋较多,这对按正常使用极限状态对构件进行验算有利。
(4)规范8.2.1条中挠度计算时对构件刚度取值的规定系根据等截面构件计算比较得到,但符合刚度比条件的变截面梁也适用,请考生注意。
