某高层剪力墙结构住宅,非抗震设计,γ =1.0;其中一矩形截面剪力墙墙肢,墙宽b=200mm,墙长h=4000mm,所承受轴向压力设计值N=6000kN,弯矩设计值M=6500kN·m;混凝土强度等级C30,暗柱内的纵向受力钢筋及墙体内的分布钢筋均采用HRB335级钢筋;竖向分布钢筋为每侧18φ8@200,暗柱采用对称配筋;设偏心距增大系数η=1.0,问暗柱内配筋与下列哪一个数值最为接近?(注:按《混凝土结构设计规范》计算)
=1.0;其中一矩形截面剪力墙墙肢,墙宽b=200mm,墙长h=4000mm,所承受轴向压力设计值N=6000kN,弯矩设计值M=6500kN·m;混凝土强度等级C30,暗柱内的纵向受力钢筋及墙体内的分布钢筋均采用HRB335级钢筋;竖向分布钢筋为每侧18φ8@200,暗柱采用对称配筋;设偏心距增大系数η=1.0,问暗柱内配筋与下列哪一个数值最为接近?(注:按《混凝土结构设计规范》计算)
 =1.0;其中一矩形截面剪力墙墙肢,墙宽b=200mm,墙长h=4000mm,所承受轴向压力设计值N=6000kN,弯矩设计值M=6500kN·m;混凝土强度等级C30,暗柱内的纵向受力钢筋及墙体内的分布钢筋均采用HRB335级钢筋;竖向分布钢筋为每侧18φ8@200,暗柱采用对称配筋;设偏心距增大系数η=1.0,问暗柱内配筋与下列哪一个数值最为接近?(注:按《混凝土结构设计规范》计算)
=1.0;其中一矩形截面剪力墙墙肢,墙宽b=200mm,墙长h=4000mm,所承受轴向压力设计值N=6000kN,弯矩设计值M=6500kN·m;混凝土强度等级C30,暗柱内的纵向受力钢筋及墙体内的分布钢筋均采用HRB335级钢筋;竖向分布钢筋为每侧18φ8@200,暗柱采用对称配筋;设偏心距增大系数η=1.0,问暗柱内配筋与下列哪一个数值最为接近?(注:按《混凝土结构设计规范》计算) 正确答案:
B
答案解析:
【主要解答过程如下】:(1)复核竖向分布钢筋的配筋率
ρ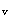 =2×50.3/200×200=0.2515%
=2×50.3/200×200=0.2515%
根据《高层建筑混凝土结构技术规程》7.2.18条,非抗震设计时,竖向分布钢筋的配筋率不应小于0.2%。故实配竖向分布钢筋符合规程要求,可参与受力。
(2)计算几何参数
从该规程7.2.15条,非抗震设计的剪力墙墙肢端部应设置构造边缘构件,暗柱的长度应≥b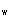 ,且≥400mm;因此确定暗柱的长度为400mm。
,且≥400mm;因此确定暗柱的长度为400mm。
于是按《混凝土结构设计规范》7.3.6条,确定几何参数如下:
α =α′
=α′ =200mm
=200mm
h =4000-α
=4000-α =4000-200=3800mm
=4000-200=3800mm
h =h
=h -α′
-α′ =3800-200=3600mm
=3800-200=3600mm
ω=h /h
/h =3600/3800=0.947
=3600/3800=0.947
A =18×2×50.3=1811mm
=18×2×50.3=1811mm
(3)计算e值
e =M/N=6500×10
=M/N=6500×10 /6000×10
/6000×10 =1083mm
=1083mm
依据规范7.3.3条
附加偏心距e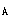 =h/30=4000/30=133mm
=h/30=4000/30=133mm
e =e
=e +e
+e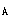 =1083+133=1216mm
=1083+133=1216mm
e=ηe +h/2-α
+h/2-α =1.0×1216+4000/2-200=3016mm
=1.0×1216+4000/2-200=3016mm
(4)计算ξ值
按规范公式(7.3.6-3)
N =(1+ξ-β
=(1+ξ-β /0.5β
/0.5β ω)f
ω)f A
A =(1+ξ-0.8/0.5×0.8×0.947)×300×1811=1434266ξ-604113
=(1+ξ-0.8/0.5×0.8×0.947)×300×1811=1434266ξ-604113
把N 代入式(7.3.6-1),并先假定按大偏压考虑;则σ
代入式(7.3.6-1),并先假定按大偏压考虑;则σ =f
=f ,σ
,σ A
A =f
=f A
A =f′
=f′ A′
A′ ,于是得到:
,于是得到:
N=6000×10 =α
=α f
f ξbh
ξbh +N
+N =1.0×14.3×200×3800ξ+1434266ξ-604113=12302266ξ-604113
=1.0×14.3×200×3800ξ+1434266ξ-604113=12302266ξ-604113
解出ξ=0.537<ξ =0.55确系大偏心受压构件。
=0.55确系大偏心受压构件。
(5)计算配筋A =A′
=A′
由规范公式(7.3.6-4)
M =[0.5-(ξ-β
=[0.5-(ξ-β /β
/β ω)]
ω)] f
f A
A h
h =[0.5-(0.537-0.8/0.8×0.947)
=[0.5-(0.537-0.8/0.8×0.947) ]×300×1811×3600=742232300N·mm
]×300×1811×3600=742232300N·mm
将M 代入公式(7.3.6-2)得:
代入公式(7.3.6-2)得:
N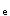 =6000×10
=6000×10 ×3016=α
×3016=α f
f ξ(1-0.5ξ)bh
ξ(1-0.5ξ)bh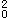 +f′
+f′ A′
A′ (h
(h -a′
-a′ )+M
)+M
=1.0×14.3×0.537×(1-0.5×0.537)×200×3800 +742232300+300A′
+742232300+300A′ ×(3800-200)=1.694883×10
×(3800-200)=1.694883×10 +1080000A′
+1080000A′
A =A′
=A′ =1047mm
=1047mm
这就是答案B。其余A、C、D都不正确。
【点评】:(1)关于非抗震设计时剪力墙墙肢端部边缘构件设置的问题,对高层建筑,《高层建筑混凝土结构技术规程》7.2.15条明确规定墙肢端部应设置构造边缘构件,并在7.2.17条对构造边缘构件的尺寸及配筋作出了规定(≥4 12)。对一般多层建筑,规范并未要求设置构造边缘构件,《混凝土结构设计规范》在10.5节墙的部分中也无任何规定,仅在10.5.8条中明确:剪力墙墙肢两端应配置竖向受力钢筋;每端竖向钢筋不宜少于4根直径为12mm的钢筋或2根直径为16mm的钢筋。进一步印证了不需设置构造边缘构件,因为允许配置2
12)。对一般多层建筑,规范并未要求设置构造边缘构件,《混凝土结构设计规范》在10.5节墙的部分中也无任何规定,仅在10.5.8条中明确:剪力墙墙肢两端应配置竖向受力钢筋;每端竖向钢筋不宜少于4根直径为12mm的钢筋或2根直径为16mm的钢筋。进一步印证了不需设置构造边缘构件,因为允许配置2 16钢筋是不可能形成边缘构件的。此外,从设置边缘构件的作用上来看,对非抗震设计,也无必要。
16钢筋是不可能形成边缘构件的。此外,从设置边缘构件的作用上来看,对非抗震设计,也无必要。
(2)在偏心受压墙肢正截面受压承载力计算中一定会涉及偏心距增大系数77的计算,这实际上是在其承载力计算中考虑结构侧移和构件挠曲引起的附加内力,即二阶效应的计算。关于框架柱已经研究得较多了,并已订入规范中。《混凝土结构设计规范》7.3.9条规定:在确定偏心受压构件的内力设计值时,可近似考虑二阶弯矩对轴向压力偏心距的影响,将轴向压力对截面重心的初始偏心距e 乘以规范7.3.10条规定的偏心距增大系数η(即η-ι
乘以规范7.3.10条规定的偏心距增大系数η(即η-ι 方法);也可根据规范7.3.12条规定的构件修正抗弯刚度,用考虑二阶效应的弹性分析方法,直接计算出结构构件各控制截面包括弯矩设计值在内的内力值,并按相应的内力设计值进行各构件的截面设计。
方法);也可根据规范7.3.12条规定的构件修正抗弯刚度,用考虑二阶效应的弹性分析方法,直接计算出结构构件各控制截面包括弯矩设计值在内的内力值,并按相应的内力设计值进行各构件的截面设计。
对于剪力墙墙肢,η-ι 法当前是不可能采用的,因为规范并未提供墙肢计算长度的计算方法;因此按规范只有采用7.3.12条考虑二阶效应的弹性分析方法了。该条条文中还规定了对各类构件的弹性抗弯刚度的不同折减系数。
法当前是不可能采用的,因为规范并未提供墙肢计算长度的计算方法;因此按规范只有采用7.3.12条考虑二阶效应的弹性分析方法了。该条条文中还规定了对各类构件的弹性抗弯刚度的不同折减系数。
《高层建筑混凝土结构技术规程》7.2.8条给出了非抗震设计时偏心受压剪力墙的正截面受压承载力计算公式。
N≤A′ f′
f′ -A
-A a
a -N
-N +N
+N (1-12-1)
(1-12-1)
N(e +h
+h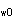 -h
-h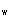 /2)≤A′
/2)≤A′ f′
f′ (h
(h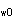 -a′
-a′ )-M
)-M +M
+M (1-12-2)
(1-12-2)
式(1-12-2)左端括号内(e +h
+h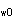 -h
-h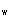 /2)=e
/2)=e +h
+h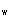 /2-a
/2-a 与《混凝土结构设计规范》式(7.3.4-3)中的e=ηe
与《混凝土结构设计规范》式(7.3.4-3)中的e=ηe +h
+h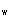 /2-a
/2-a =θ(e
=θ(e +e
+e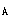 +h
+h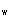 /2-a
/2-a 相比较,高规中取η=1.0,e
相比较,高规中取η=1.0,e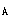 =0。显然取η=1.0,即认为对剪力墙墙肢,二阶效应对其内力影响甚微,可以忽略不计。
=0。显然取η=1.0,即认为对剪力墙墙肢,二阶效应对其内力影响甚微,可以忽略不计。
(3)附加偏心距e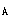 的取值在《混凝土结构设计规范》7.3.3条中有明确的规定,但在高规中不予考虑,这确实值得商量,因为附加偏心距是客观存在,但对剪力墙墙肢而言其取值是否偏大,则也有这种可能;以本题为例,对4000mm长度的墙肢而言,e
的取值在《混凝土结构设计规范》7.3.3条中有明确的规定,但在高规中不予考虑,这确实值得商量,因为附加偏心距是客观存在,但对剪力墙墙肢而言其取值是否偏大,则也有这种可能;以本题为例,对4000mm长度的墙肢而言,e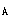 =133mm,可能大了一些,但在当前规范的条文规定下,对剪力墙墙肢还是应当取e
=133mm,可能大了一些,但在当前规范的条文规定下,对剪力墙墙肢还是应当取e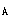 =max(20,h/30)。
=max(20,h/30)。
ρ
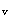 =2×50.3/200×200=0.2515%
=2×50.3/200×200=0.2515%根据《高层建筑混凝土结构技术规程》7.2.18条,非抗震设计时,竖向分布钢筋的配筋率不应小于0.2%。故实配竖向分布钢筋符合规程要求,可参与受力。
(2)计算几何参数
从该规程7.2.15条,非抗震设计的剪力墙墙肢端部应设置构造边缘构件,暗柱的长度应≥b
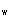 ,且≥400mm;因此确定暗柱的长度为400mm。
,且≥400mm;因此确定暗柱的长度为400mm。于是按《混凝土结构设计规范》7.3.6条,确定几何参数如下:
α
 =α′
=α′ =200mm
=200mmh
 =4000-α
=4000-α =4000-200=3800mm
=4000-200=3800mmh
 =h
=h -α′
-α′ =3800-200=3600mm
=3800-200=3600mmω=h
 /h
/h =3600/3800=0.947
=3600/3800=0.947A
 =18×2×50.3=1811mm
=18×2×50.3=1811mm
(3)计算e值
e
 =M/N=6500×10
=M/N=6500×10 /6000×10
/6000×10 =1083mm
=1083mm依据规范7.3.3条
附加偏心距e
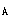 =h/30=4000/30=133mm
=h/30=4000/30=133mme
 =e
=e +e
+e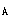 =1083+133=1216mm
=1083+133=1216mme=ηe
 +h/2-α
+h/2-α =1.0×1216+4000/2-200=3016mm
=1.0×1216+4000/2-200=3016mm(4)计算ξ值
按规范公式(7.3.6-3)
N
 =(1+ξ-β
=(1+ξ-β /0.5β
/0.5β ω)f
ω)f A
A =(1+ξ-0.8/0.5×0.8×0.947)×300×1811=1434266ξ-604113
=(1+ξ-0.8/0.5×0.8×0.947)×300×1811=1434266ξ-604113把N
 代入式(7.3.6-1),并先假定按大偏压考虑;则σ
代入式(7.3.6-1),并先假定按大偏压考虑;则σ =f
=f ,σ
,σ A
A =f
=f A
A =f′
=f′ A′
A′ ,于是得到:
,于是得到:N=6000×10
 =α
=α f
f ξbh
ξbh +N
+N =1.0×14.3×200×3800ξ+1434266ξ-604113=12302266ξ-604113
=1.0×14.3×200×3800ξ+1434266ξ-604113=12302266ξ-604113解出ξ=0.537<ξ
 =0.55确系大偏心受压构件。
=0.55确系大偏心受压构件。(5)计算配筋A
 =A′
=A′
由规范公式(7.3.6-4)
M
 =[0.5-(ξ-β
=[0.5-(ξ-β /β
/β ω)]
ω)] f
f A
A h
h =[0.5-(0.537-0.8/0.8×0.947)
=[0.5-(0.537-0.8/0.8×0.947) ]×300×1811×3600=742232300N·mm
]×300×1811×3600=742232300N·mm将M
 代入公式(7.3.6-2)得:
代入公式(7.3.6-2)得:N
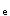 =6000×10
=6000×10 ×3016=α
×3016=α f
f ξ(1-0.5ξ)bh
ξ(1-0.5ξ)bh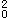 +f′
+f′ A′
A′ (h
(h -a′
-a′ )+M
)+M
=1.0×14.3×0.537×(1-0.5×0.537)×200×3800
 +742232300+300A′
+742232300+300A′ ×(3800-200)=1.694883×10
×(3800-200)=1.694883×10 +1080000A′
+1080000A′
A
 =A′
=A′ =1047mm
=1047mm
这就是答案B。其余A、C、D都不正确。
【点评】:(1)关于非抗震设计时剪力墙墙肢端部边缘构件设置的问题,对高层建筑,《高层建筑混凝土结构技术规程》7.2.15条明确规定墙肢端部应设置构造边缘构件,并在7.2.17条对构造边缘构件的尺寸及配筋作出了规定(≥4
 12)。对一般多层建筑,规范并未要求设置构造边缘构件,《混凝土结构设计规范》在10.5节墙的部分中也无任何规定,仅在10.5.8条中明确:剪力墙墙肢两端应配置竖向受力钢筋;每端竖向钢筋不宜少于4根直径为12mm的钢筋或2根直径为16mm的钢筋。进一步印证了不需设置构造边缘构件,因为允许配置2
12)。对一般多层建筑,规范并未要求设置构造边缘构件,《混凝土结构设计规范》在10.5节墙的部分中也无任何规定,仅在10.5.8条中明确:剪力墙墙肢两端应配置竖向受力钢筋;每端竖向钢筋不宜少于4根直径为12mm的钢筋或2根直径为16mm的钢筋。进一步印证了不需设置构造边缘构件,因为允许配置2 16钢筋是不可能形成边缘构件的。此外,从设置边缘构件的作用上来看,对非抗震设计,也无必要。
16钢筋是不可能形成边缘构件的。此外,从设置边缘构件的作用上来看,对非抗震设计,也无必要。(2)在偏心受压墙肢正截面受压承载力计算中一定会涉及偏心距增大系数77的计算,这实际上是在其承载力计算中考虑结构侧移和构件挠曲引起的附加内力,即二阶效应的计算。关于框架柱已经研究得较多了,并已订入规范中。《混凝土结构设计规范》7.3.9条规定:在确定偏心受压构件的内力设计值时,可近似考虑二阶弯矩对轴向压力偏心距的影响,将轴向压力对截面重心的初始偏心距e
 乘以规范7.3.10条规定的偏心距增大系数η(即η-ι
乘以规范7.3.10条规定的偏心距增大系数η(即η-ι 方法);也可根据规范7.3.12条规定的构件修正抗弯刚度,用考虑二阶效应的弹性分析方法,直接计算出结构构件各控制截面包括弯矩设计值在内的内力值,并按相应的内力设计值进行各构件的截面设计。
方法);也可根据规范7.3.12条规定的构件修正抗弯刚度,用考虑二阶效应的弹性分析方法,直接计算出结构构件各控制截面包括弯矩设计值在内的内力值,并按相应的内力设计值进行各构件的截面设计。对于剪力墙墙肢,η-ι
 法当前是不可能采用的,因为规范并未提供墙肢计算长度的计算方法;因此按规范只有采用7.3.12条考虑二阶效应的弹性分析方法了。该条条文中还规定了对各类构件的弹性抗弯刚度的不同折减系数。
法当前是不可能采用的,因为规范并未提供墙肢计算长度的计算方法;因此按规范只有采用7.3.12条考虑二阶效应的弹性分析方法了。该条条文中还规定了对各类构件的弹性抗弯刚度的不同折减系数。《高层建筑混凝土结构技术规程》7.2.8条给出了非抗震设计时偏心受压剪力墙的正截面受压承载力计算公式。
N≤A′
 f′
f′ -A
-A a
a -N
-N +N
+N (1-12-1)
(1-12-1)N(e
 +h
+h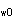 -h
-h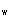 /2)≤A′
/2)≤A′ f′
f′ (h
(h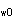 -a′
-a′ )-M
)-M +M
+M (1-12-2)
(1-12-2)式(1-12-2)左端括号内(e
 +h
+h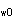 -h
-h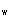 /2)=e
/2)=e +h
+h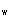 /2-a
/2-a 与《混凝土结构设计规范》式(7.3.4-3)中的e=ηe
与《混凝土结构设计规范》式(7.3.4-3)中的e=ηe +h
+h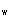 /2-a
/2-a =θ(e
=θ(e +e
+e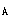 +h
+h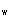 /2-a
/2-a 相比较,高规中取η=1.0,e
相比较,高规中取η=1.0,e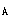 =0。显然取η=1.0,即认为对剪力墙墙肢,二阶效应对其内力影响甚微,可以忽略不计。
=0。显然取η=1.0,即认为对剪力墙墙肢,二阶效应对其内力影响甚微,可以忽略不计。(3)附加偏心距e
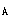 的取值在《混凝土结构设计规范》7.3.3条中有明确的规定,但在高规中不予考虑,这确实值得商量,因为附加偏心距是客观存在,但对剪力墙墙肢而言其取值是否偏大,则也有这种可能;以本题为例,对4000mm长度的墙肢而言,e
的取值在《混凝土结构设计规范》7.3.3条中有明确的规定,但在高规中不予考虑,这确实值得商量,因为附加偏心距是客观存在,但对剪力墙墙肢而言其取值是否偏大,则也有这种可能;以本题为例,对4000mm长度的墙肢而言,e =133mm,可能大了一些,但在当前规范的条文规定下,对剪力墙墙肢还是应当取e
=133mm,可能大了一些,但在当前规范的条文规定下,对剪力墙墙肢还是应当取e =max(20,h/30)。
=max(20,h/30)。