一矩形截面钢筋混凝土柱,柱截面尺寸b=400mm,h=450mm,柱净高h =3.5m,内配有8φ25钢筋(图1-13-1);经计算轴向压力设计值N=890kN,斜向剪力设计值V=200kN,剪力作用方向与x轴的夹角θ=30°,弯矩反弯点在层高范围内,非抗震设计,γ
=3.5m,内配有8φ25钢筋(图1-13-1);经计算轴向压力设计值N=890kN,斜向剪力设计值V=200kN,剪力作用方向与x轴的夹角θ=30°,弯矩反弯点在层高范围内,非抗震设计,γ =1.0;b
=1.0;b =360mm,h
=360mm,h =410mm;混凝土强度等级C30,箍筋采用HRB335级钢筋。箍筋采用下列何种配置最为合理?
=410mm;混凝土强度等级C30,箍筋采用HRB335级钢筋。箍筋采用下列何种配置最为合理?

 =3.5m,内配有8φ25钢筋(图1-13-1);经计算轴向压力设计值N=890kN,斜向剪力设计值V=200kN,剪力作用方向与x轴的夹角θ=30°,弯矩反弯点在层高范围内,非抗震设计,γ
=3.5m,内配有8φ25钢筋(图1-13-1);经计算轴向压力设计值N=890kN,斜向剪力设计值V=200kN,剪力作用方向与x轴的夹角θ=30°,弯矩反弯点在层高范围内,非抗震设计,γ =1.0;b
=1.0;b =360mm,h
=360mm,h =410mm;混凝土强度等级C30,箍筋采用HRB335级钢筋。箍筋采用下列何种配置最为合理?
=410mm;混凝土强度等级C30,箍筋采用HRB335级钢筋。箍筋采用下列何种配置最为合理?
正确答案:
B
答案解析:
【主要解答过程如下】:(1)求V 、V
、V ,
,
V =Vcosθ=200×cos30°=173.2kN
=Vcosθ=200×cos30°=173.2kN
V =Vsinθ=200×sin30°=100kN
=Vsinθ=200×sin30°=100kN
(2)复核截面控制条件
根据《混凝土结构设计规范》7.5.16条,柱截面尺寸应符合下列要求:
0.25×1.0×14.3×400×410cos30°=508×10 N=508kN>V
N=508kN>V
0.25×1.0×14.3×450×360sin30°=290×10 N=290kN>V
N=290kN>V
均符合要求。
(3)斜截面受剪承载力计算
按规范7.5.17条,并近似取V /V
/V =1.0,tanθ=tan30°=0.577则,V
=1.0,tanθ=tan30°=0.577则,V ≤
≤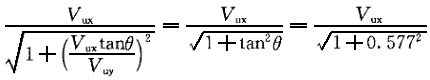 =0.866V
=0.866V
V =V
=V 1/0.866=1.155V
1/0.866=1.155V =200kN
=200kN
V =
= =2V
=2V =200kN
=200kN
λ =H
=H /2h
/2h =3500/2×410=4.27>3,取λ
=3500/2×410=4.27>3,取λ =3.0
=3.0
λ =H
=H /2h
/2h =3500/2×360=4.86>3,取λ
=3500/2×360=4.86>3,取λ =3.0
=3.0
依据公式(7.5.17-3)(7.5.17-4)计算配箍
V =1.75/λ
=1.75/λ f
f bh
bh +f
+f A
A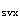 +0.07N
+0.07N
V =1.75/λ
=1.75/λ f
f bh
bh +f
+f A
A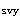 +0.07N
+0.07N
0.3f A=0.3×14.3×400×450=772200N=772.2kN<890kN
A=0.3×14.3×400×450=772200N=772.2kN<890kN
取N=772.2kN
A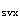 /s=1/f
/s=1/f h
h [V
[V -1.75f
-1.75f bh
bh /λ
/λ -0.07N]
-0.07N]
=1/300×410[200×10 -(1.75/3.0+1)×1.43×400×410-0.07×772.2×10
-(1.75/3.0+1)×1.43×400×410-0.07×772.2×10 ]
]
=0.3524mm /mm
/mm
从规范10.3.2条,箍筋直径不应小于d/4=25/4=6.25mm,并根据该条第5款,当柱截面短边尺寸不大于400mm,仅当各边纵向钢筋多于4根时,方应设置复合箍筋。因此可选用双肢箍,且箍筋直径为 8。
8。
s=50.3×2/0.3524=285mm
A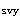 /s=1/f
/s=1/f h
h [V
[V -1.75f
-1.75f bh
bh /λ
/λ -0.07N]
-0.07N]
=1/300×360[200×10 -(1.75/3.0+1)×1.43×400×410-0.07×772.2×10
-(1.75/3.0+1)×1.43×400×410-0.07×772.2×10 ]=0.413mm
]=0.413mm /mm
/mm
s=50.3×2/0.413=243mm
纵向钢筋配筋率ρ=8×490.9/400×450=2.18%<3%
所以箍筋选用2 8@240,箍筋间距亦符合规范10.3.2条2款的要求。
8@240,箍筋间距亦符合规范10.3.2条2款的要求。
选项B是正确的。A则是箍筋抗剪能力不足,C与D均是箍筋直径不符合规范规定。
【点评】:(1)试验表明,矩形截面钢筋混凝土柱在斜向水平力作用下的抗剪性能与在单向水平力作用下的抗剪性能存在明显的差别,国内外的试验分析说明,其受剪承载力大致符合椭圆规律。
(V /V
/V )
) +(V
+(V /V
/V )
) =1(1-13-1)
=1(1-13-1)
式中V 、V
、V 为单向受力的斜截面受剪承载力设计值,即规范公式(7.5.17-3)
为单向受力的斜截面受剪承载力设计值,即规范公式(7.5.17-3)
V =1.75/λ
=1.75/λ f
f bh
bh +f
+f A
A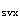 +0.07N(1-13-2)
+0.07N(1-13-2)
V =1.75/λ
=1.75/λ f
f bh
bh +f
+f A
A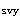 +0.07N(1-13-3)
+0.07N(1-13-3)
从椭圆方程出发,可得到规范公式(7.5.17-1)(7.5.17-2),
V ≤
≤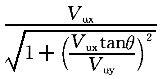 V
V ≤
≤ (1-13-4)
(1-13-4)
此二式作为复核公式可以,但无法进行设计。近似取A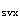 =b
=b A
A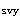 /h
/h ,并近似认为bh
,并近似认为bh ≈hb
≈hb ,将其代入式(1-13-2)(1-13-3),并忽略λ
,将其代入式(1-13-2)(1-13-3),并忽略λ ≠λ
≠λ ,得到V
,得到V ≈V
≈V ,推得V
,推得V /V
/V =1.0再代入式(1-13-4),得到:
=1.0再代入式(1-13-4),得到:
V ≤
≤ =V
=V cosθ
cosθ
V ≤
≤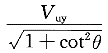 =V
=V sinθ
sinθ
于是斜向剪力可以分解为V 、V
、V 单独进行受剪承载力计算,各不相关。
单独进行受剪承载力计算,各不相关。
受剪截面控制条件在单方向水平力作用下
应为:V ≤0.25β
≤0.25β f
f bh
bh V
V ≤0.25β
≤0.25β f
f bh
bh
等式右边可近似视为V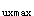 =0.25β
=0.25β f
f bh
bh
V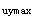 =0.25β
=0.25β f
f bh
bh
并近似取bh =hb
=hb 代入式(1-134)即得:
代入式(1-134)即得:
V ≤0.25β
≤0.25β f
f bh
bh cosθ,V
cosθ,V ≤0.25V
≤0.25V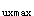 =0.25β
=0.25β f
f bh
bh sinθ
sinθ
此即规范公式(7.5.16-1)及(7.5.16-2)。
(2)矩形截面双向受剪的斜截面受剪承载力计算公式仅适用于非抗震设计,抗震设计尚未有计算公式。为了弥补不足,《高层建筑混凝土结构技术规程》6.2.4条规定:"框架角柱应按双向偏心受力构件进行正截面承载力设计。一、二、三级框架角柱需按本规程第6.2.1~6.2.3条调整后的弯矩、剪力设计值应乘以不小于1.1的增大系数。"即明确了角柱的正截面承载力按双向偏心受压构件计算,受剪隐含了将剪力放大后,可按单向受剪计算斜截面受剪承载力。
 、V
、V ,
,V
 =Vcosθ=200×cos30°=173.2kN
=Vcosθ=200×cos30°=173.2kNV
 =Vsinθ=200×sin30°=100kN
=Vsinθ=200×sin30°=100kN(2)复核截面控制条件
根据《混凝土结构设计规范》7.5.16条,柱截面尺寸应符合下列要求:
0.25×1.0×14.3×400×410cos30°=508×10
 N=508kN>V
N=508kN>V
0.25×1.0×14.3×450×360sin30°=290×10
 N=290kN>V
N=290kN>V
均符合要求。
(3)斜截面受剪承载力计算
按规范7.5.17条,并近似取V
 /V
/V =1.0,tanθ=tan30°=0.577则,V
=1.0,tanθ=tan30°=0.577则,V ≤
≤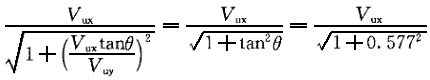 =0.866V
=0.866V
V
 =V
=V 1/0.866=1.155V
1/0.866=1.155V =200kN
=200kNV
 =
= =2V
=2V =200kN
=200kNλ
 =H
=H /2h
/2h =3500/2×410=4.27>3,取λ
=3500/2×410=4.27>3,取λ =3.0
=3.0λ
 =H
=H /2h
/2h =3500/2×360=4.86>3,取λ
=3500/2×360=4.86>3,取λ =3.0
=3.0依据公式(7.5.17-3)(7.5.17-4)计算配箍
V
 =1.75/λ
=1.75/λ f
f bh
bh +f
+f A
A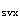 +0.07N
+0.07NV
 =1.75/λ
=1.75/λ f
f bh
bh +f
+f A
A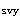 +0.07N
+0.07N0.3f
 A=0.3×14.3×400×450=772200N=772.2kN<890kN
A=0.3×14.3×400×450=772200N=772.2kN<890kN取N=772.2kN
A
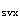 /s=1/f
/s=1/f h
h [V
[V -1.75f
-1.75f bh
bh /λ
/λ -0.07N]
-0.07N]=1/300×410[200×10
 -(1.75/3.0+1)×1.43×400×410-0.07×772.2×10
-(1.75/3.0+1)×1.43×400×410-0.07×772.2×10 ]
]=0.3524mm
 /mm
/mm从规范10.3.2条,箍筋直径不应小于d/4=25/4=6.25mm,并根据该条第5款,当柱截面短边尺寸不大于400mm,仅当各边纵向钢筋多于4根时,方应设置复合箍筋。因此可选用双肢箍,且箍筋直径为
 8。
8。s=50.3×2/0.3524=285mm
A
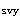 /s=1/f
/s=1/f h
h [V
[V -1.75f
-1.75f bh
bh /λ
/λ -0.07N]
-0.07N]=1/300×360[200×10
 -(1.75/3.0+1)×1.43×400×410-0.07×772.2×10
-(1.75/3.0+1)×1.43×400×410-0.07×772.2×10 ]=0.413mm
]=0.413mm /mm
/mms=50.3×2/0.413=243mm
纵向钢筋配筋率ρ=8×490.9/400×450=2.18%<3%
所以箍筋选用2
 8@240,箍筋间距亦符合规范10.3.2条2款的要求。
8@240,箍筋间距亦符合规范10.3.2条2款的要求。选项B是正确的。A则是箍筋抗剪能力不足,C与D均是箍筋直径不符合规范规定。
【点评】:(1)试验表明,矩形截面钢筋混凝土柱在斜向水平力作用下的抗剪性能与在单向水平力作用下的抗剪性能存在明显的差别,国内外的试验分析说明,其受剪承载力大致符合椭圆规律。
(V
 /V
/V )
) +(V
+(V /V
/V )
) =1(1-13-1)
=1(1-13-1)式中V
 、V
、V 为单向受力的斜截面受剪承载力设计值,即规范公式(7.5.17-3)
为单向受力的斜截面受剪承载力设计值,即规范公式(7.5.17-3)V
 =1.75/λ
=1.75/λ f
f bh
bh +f
+f A
A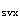 +0.07N(1-13-2)
+0.07N(1-13-2)V
 =1.75/λ
=1.75/λ f
f bh
bh +f
+f A
A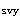 +0.07N(1-13-3)
+0.07N(1-13-3)从椭圆方程出发,可得到规范公式(7.5.17-1)(7.5.17-2),
V
 ≤
≤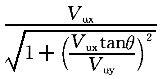 V
V ≤
≤ (1-13-4)
(1-13-4)此二式作为复核公式可以,但无法进行设计。近似取A
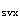 =b
=b A
A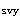 /h
/h ,并近似认为bh
,并近似认为bh ≈hb
≈hb ,将其代入式(1-13-2)(1-13-3),并忽略λ
,将其代入式(1-13-2)(1-13-3),并忽略λ ≠λ
≠λ ,得到V
,得到V ≈V
≈V ,推得V
,推得V /V
/V =1.0再代入式(1-13-4),得到:
=1.0再代入式(1-13-4),得到:V
 ≤
≤ =V
=V cosθ
cosθV
 ≤
≤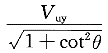 =V
=V sinθ
sinθ于是斜向剪力可以分解为V
 、V
、V 单独进行受剪承载力计算,各不相关。
单独进行受剪承载力计算,各不相关。受剪截面控制条件在单方向水平力作用下
应为:V
 ≤0.25β
≤0.25β f
f bh
bh V
V ≤0.25β
≤0.25β f
f bh
bh
等式右边可近似视为V
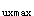 =0.25β
=0.25β f
f bh
bh
V
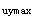 =0.25β
=0.25β f
f bh
bh
并近似取bh
 =hb
=hb 代入式(1-134)即得:
代入式(1-134)即得:V
 ≤0.25β
≤0.25β f
f bh
bh cosθ,V
cosθ,V ≤0.25V
≤0.25V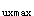 =0.25β
=0.25β f
f bh
bh sinθ
sinθ此即规范公式(7.5.16-1)及(7.5.16-2)。
(2)矩形截面双向受剪的斜截面受剪承载力计算公式仅适用于非抗震设计,抗震设计尚未有计算公式。为了弥补不足,《高层建筑混凝土结构技术规程》6.2.4条规定:"框架角柱应按双向偏心受力构件进行正截面承载力设计。一、二、三级框架角柱需按本规程第6.2.1~6.2.3条调整后的弯矩、剪力设计值应乘以不小于1.1的增大系数。"即明确了角柱的正截面承载力按双向偏心受压构件计算,受剪隐含了将剪力放大后,可按单向受剪计算斜截面受剪承载力。
