计算在结构尺寸图图1-11-1中,中柱KZ-3在Y方向地震作用下底层柱的配筋。其中柱截面尺寸为700mm×700mm,二层框架梁KL-2的截面尺寸为300mm×700mm(考虑楼板的作用,梁刚度增大系数取2.0);楼层层高见图1-11-1;混凝土强度等级,梁为C25,柱为C30,采用HRB400级钢筋。

经计算柱控制截面的弯矩设计值M=1100kN·m,轴向压力设计值N=3700kN,且地震作用产生的弯矩设计值占总弯矩设计值的75%以上;h =655mm。最小相对界限偏心距C
=655mm。最小相对界限偏心距C /h
/h 列入表中,采用对称配筋。
列入表中,采用对称配筋。

问柱配筋A =A′
=A′ ,下列哪一个数值最为接近?
,下列哪一个数值最为接近?

经计算柱控制截面的弯矩设计值M=1100kN·m,轴向压力设计值N=3700kN,且地震作用产生的弯矩设计值占总弯矩设计值的75%以上;h
 =655mm。最小相对界限偏心距C
=655mm。最小相对界限偏心距C /h
/h 列入表中,采用对称配筋。
列入表中,采用对称配筋。
问柱配筋A
 =A′
=A′ ,下列哪一个数值最为接近?
,下列哪一个数值最为接近? 正确答案:
D
答案解析:
【主要解答过程如下】:(1)计算柱的计算长度ι
因地震作用产生的弯矩设计值占总弯矩设计值75%以上,根据《混凝土结构设计规范》7.3.11条,ι 需经计算确定。
需经计算确定。
柱上端节点处梁KL-2的线刚度为:
E I
I /8000=2.8×10
/8000=2.8×10 ×(1/12)×300×700
×(1/12)×300×700 ×2/8000=6.0×10
×2/8000=6.0×10 N·mm
N·mm
柱上端节点处上部柱的线刚度为:
E I
I /8000=3.0×10
/8000=3.0×10 ×(1/12)×700
×(1/12)×700 /5000=12×10
/5000=12×10 N·mm
N·mm
柱上端节点处下部柱的线刚度为:
E I
I /6000=3.0×10
/6000=3.0×10 ×(1/12)×700
×(1/12)×700 /6000=10×10
/6000=10×10 N·mm
N·mm
按照规范7.3.11条3款
ψ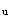 =12×10
=12×10 ×10×10
×10×10 /2×6.0×10
/2×6.0×10 =1.833,ψ
=1.833,ψ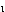 =0
=0
从公式(7.3.11-1),ι =(1+0.15×1.833)×6000=7650mm
=(1+0.15×1.833)×6000=7650mm
(2)计算柱偏心距增大系数
ζ =0.5f
=0.5f A/N=0.5×14.3×700×700/3700×10
A/N=0.5×14.3×700×700/3700×10 =0.947
=0.947
ι /h=7650/700=10.93<15,取ζ
/h=7650/700=10.93<15,取ζ =1.0
=1.0
e =M/N=1100/3700=0.297m
=M/N=1100/3700=0.297m
依据规范7.3.3条,附加偏心距e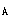 =max(20,700/30)=23mm,e
=max(20,700/30)=23mm,e =297+23=320mm
=297+23=320mm
于是由规范公式(7.3.10-1)得到:
η=1+1/1400e /h
/h (ι
(ι /h)
/h) ζ
ζ ·ζ
·ζ
=1+1/1400×320/655(10.93) ×0.947×1.0=1.165
×0.947×1.0=1.165
(3)计算配筋
η =1.165×320=372.8mm
=1.165×320=372.8mm
从表1-11-1中查到对应于C30及HRB400级钢筋的最小相对界限偏心距为0.363。
e =0.363×655=237.8mm
=0.363×655=237.8mm
ηe >e
>e
对应于HRB400级钢筋及C30的相对界限受压区高度ξ 可从规范公式(7.1.4-1)计算得到。
可从规范公式(7.1.4-1)计算得到。
ξ =0.8/1+360/2.0×10
=0.8/1+360/2.0×10 ×0.0033=0.518
×0.0033=0.518
N =α
=α f
f bh
bh ξ
ξ =1.0×14.3×700×655×0.518=3396293N
=1.0×14.3×700×655×0.518=3396293N
因此查规范表11.1.6,γ =0.8
=0.8
γ N=0.8×3700=2960kN<N
N=0.8×3700=2960kN<N
因为ηe >e
>e ,且γ
,且γ N<N
N<N 判断为大偏心受压(见本题【点评】)。
判断为大偏心受压(见本题【点评】)。
从规范公式(7.3.4-1)、(7.3.4-2)及11.4.1条
x=γ N/α
N/α f
f b=0.8×3700×10
b=0.8×3700×10 /1.0×14.3×700=296mm>2a′
/1.0×14.3×700=296mm>2a′ =2×45=90mm
=2×45=90mm
e=ηe +h/2-α
+h/2-α =372.8+350-45=678mm
=372.8+350-45=678mm
A =A′
=A′ =γ
=γ Ne-γ
Ne-γ N(h
N(h -x/2)/f′
-x/2)/f′ (h
(h -a′
-a′ )
)
0.8×3700×10 ×678-0.8×3700×10
×678-0.8×3700×10 ×(655-296/2)=2305mm
×(655-296/2)=2305mm
又由规范表9.5.1得知,一侧纵向受力钢筋的配筋率为:
ρ=2305/700×700=0.47%>0.2%(符合要求)
因此选项D是正确的。A系根据一侧钢筋最小配筋率计算,B系按照全部纵向钢筋的最小配筋率计算,C纯属计算过程中的错误,都是不正确的。
【点评】:(1)规范7.3.4条指出:当ζ≤ζ 时为大偏心受压构件,ζ>ζ
时为大偏心受压构件,ζ>ζ 时为小偏心受压构件;由于在计算柱配筋时,A
时为小偏心受压构件;由于在计算柱配筋时,A 和A′
和A′ 均为未知,无从计算ζ,因此不能直接利用上述条件进行判别。
均为未知,无从计算ζ,因此不能直接利用上述条件进行判别。
清华大学庄崖屏、叶列平教授(均为《混凝土结构设计规范》(GB50010-2002)第7章正截面承载力计算部分的主要起草人)在规范组组织编写的《混凝土结构设计》一书中给出了如下判别方法。
取界限破坏时的受压区高度x =ζ
=ζ h
h 代入大偏心受压的计算公式(即规范公式(7.3.4-1)、(7.3.4-2),并取a=a′,即可得界限破坏时的轴力N
代入大偏心受压的计算公式(即规范公式(7.3.4-1)、(7.3.4-2),并取a=a′,即可得界限破坏时的轴力N 和弯矩M
和弯矩M 如下:
如下:
N =α
=α f
f bζ
bζ h
h +f′
+f′ A′
A′ -f
-f A
A
M =0.5α
=0.5α f
f bζ
bζ h
h (h-ζ
(h-ζ h
h )+0.5(f′
)+0.5(f′ A′
A′ +f
+f A
A )(h
)(h -a)
-a)
由此得到相对界限偏心距为:
e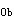 =M
=M /N
/N h
h =0.5α
=0.5α f
f bζ
bζ h
h (h-ζ
(h-ζ h
h )+0.5(f′
)+0.5(f′ A′
A′ +f
+f A
A )(h
)(h -a)/(α
-a)/(α f
f bζ
bζ h
h +f′
+f′ A′
A′ -f
-f A
A )h
)h
分析上式得知,当构件截面尺寸和材料强度设计值给定,相对界限偏心距e b/h
b/h 就取决于截面配筋A
就取决于截面配筋A 与A′
与A′ 。且随A
。且随A 与A′
与A′ 的减小,e
的减小,e b/h
b/h 也随之减小。A
也随之减小。A 与A′
与A′ 取最小配筋率时可得e
取最小配筋率时可得e b/h
b/h 的最小值e
的最小值e /h
/h 。规范规定对偏心受压构件,受拉钢筋A
。规范规定对偏心受压构件,受拉钢筋A 与受压钢筋A′
与受压钢筋A′ 按构件全截面面积计算的最小配筋率均为0.002。并近似取h=1.05h
按构件全截面面积计算的最小配筋率均为0.002。并近似取h=1.05h ,a′=0.05h代入公式(1-11-1),即可得对应于常用的各种混凝土强度等级及HRB335级和HRB400级钢筋,相对界限偏心距的最小值e
,a′=0.05h代入公式(1-11-1),即可得对应于常用的各种混凝土强度等级及HRB335级和HRB400级钢筋,相对界限偏心距的最小值e /h
/h ,即本题开题时所列入的表1-11-1中的对应数值(注:原文对受拉钢筋A
,即本题开题时所列入的表1-11-1中的对应数值(注:原文对受拉钢筋A 按构件全截面面积计算的最小配筋率为0.002和0.45f
按构件全截面面积计算的最小配筋率为0.002和0.45f /f
/f 两者中的较大者,可能系按规范中问稿的规定确定,与正式稿不符,笔者在表1-11-1中已加以改正)。当ηe
两者中的较大者,可能系按规范中问稿的规定确定,与正式稿不符,笔者在表1-11-1中已加以改正)。当ηe ≤e
≤e 时按小偏心受压构件计算;ηe
时按小偏心受压构件计算;ηe >e
>e 时,则应按式(1-11-1)求出e
时,则应按式(1-11-1)求出e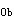 /h
/h 后再作出判别。
后再作出判别。
对于对称配筋的矩形截面构件,在清华大学滕智明教授主编的《钢筋混凝土基本构件》(第二版)一书中给出了判别方法:
N =α
=α f
f bh
bh ζ
ζ
当ηe >e
>e ,而ηe
,而ηe ≤e
≤e 且N>N
且N>N 时为小偏心受压构件;当ηe
时为小偏心受压构件;当ηe >e
>e 且N≤N
且N≤N 时为大偏心受压构件。本题即按此求解。
时为大偏心受压构件。本题即按此求解。
(2)实际上,我国过去一直采用上述方法判别两种偏心受压情况,但取e =0.3h
=0.3h ,那是建立在过去的混凝土强度水平、混凝土采用弯曲抗压强度、钢筋的品种和最小配筋率水平的基础上,现在条件变化了,自然要修改。
,那是建立在过去的混凝土强度水平、混凝土采用弯曲抗压强度、钢筋的品种和最小配筋率水平的基础上,现在条件变化了,自然要修改。

因地震作用产生的弯矩设计值占总弯矩设计值75%以上,根据《混凝土结构设计规范》7.3.11条,ι
 需经计算确定。
需经计算确定。柱上端节点处梁KL-2的线刚度为:
E
 I
I /8000=2.8×10
/8000=2.8×10 ×(1/12)×300×700
×(1/12)×300×700 ×2/8000=6.0×10
×2/8000=6.0×10 N·mm
N·mm柱上端节点处上部柱的线刚度为:
E
 I
I /8000=3.0×10
/8000=3.0×10 ×(1/12)×700
×(1/12)×700 /5000=12×10
/5000=12×10 N·mm
N·mm柱上端节点处下部柱的线刚度为:
E
 I
I /6000=3.0×10
/6000=3.0×10 ×(1/12)×700
×(1/12)×700 /6000=10×10
/6000=10×10 N·mm
N·mm按照规范7.3.11条3款
ψ
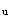 =12×10
=12×10 ×10×10
×10×10 /2×6.0×10
/2×6.0×10 =1.833,ψ
=1.833,ψ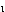 =0
=0从公式(7.3.11-1),ι
 =(1+0.15×1.833)×6000=7650mm
=(1+0.15×1.833)×6000=7650mm(2)计算柱偏心距增大系数
ζ
 =0.5f
=0.5f A/N=0.5×14.3×700×700/3700×10
A/N=0.5×14.3×700×700/3700×10 =0.947
=0.947ι
 /h=7650/700=10.93<15,取ζ
/h=7650/700=10.93<15,取ζ =1.0
=1.0e
 =M/N=1100/3700=0.297m
=M/N=1100/3700=0.297m依据规范7.3.3条,附加偏心距e
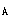 =max(20,700/30)=23mm,e
=max(20,700/30)=23mm,e =297+23=320mm
=297+23=320mm于是由规范公式(7.3.10-1)得到:
η=1+1/1400e
 /h
/h (ι
(ι /h)
/h) ζ
ζ ·ζ
·ζ
=1+1/1400×320/655(10.93)
 ×0.947×1.0=1.165
×0.947×1.0=1.165(3)计算配筋
η
 =1.165×320=372.8mm
=1.165×320=372.8mm从表1-11-1中查到对应于C30及HRB400级钢筋的最小相对界限偏心距为0.363。
e
 =0.363×655=237.8mm
=0.363×655=237.8mmηe
 >e
>e
对应于HRB400级钢筋及C30的相对界限受压区高度ξ
 可从规范公式(7.1.4-1)计算得到。
可从规范公式(7.1.4-1)计算得到。ξ
 =0.8/1+360/2.0×10
=0.8/1+360/2.0×10 ×0.0033=0.518
×0.0033=0.518N
 =α
=α f
f bh
bh ξ
ξ =1.0×14.3×700×655×0.518=3396293N
=1.0×14.3×700×655×0.518=3396293N因此查规范表11.1.6,γ
 =0.8
=0.8γ
 N=0.8×3700=2960kN<N
N=0.8×3700=2960kN<N
因为ηe
 >e
>e ,且γ
,且γ N<N
N<N 判断为大偏心受压(见本题【点评】)。
判断为大偏心受压(见本题【点评】)。从规范公式(7.3.4-1)、(7.3.4-2)及11.4.1条
x=γ
 N/α
N/α f
f b=0.8×3700×10
b=0.8×3700×10 /1.0×14.3×700=296mm>2a′
/1.0×14.3×700=296mm>2a′ =2×45=90mm
=2×45=90mme=ηe
 +h/2-α
+h/2-α =372.8+350-45=678mm
=372.8+350-45=678mmA
 =A′
=A′ =γ
=γ Ne-γ
Ne-γ N(h
N(h -x/2)/f′
-x/2)/f′ (h
(h -a′
-a′ )
)0.8×3700×10
 ×678-0.8×3700×10
×678-0.8×3700×10 ×(655-296/2)=2305mm
×(655-296/2)=2305mm
又由规范表9.5.1得知,一侧纵向受力钢筋的配筋率为:
ρ=2305/700×700=0.47%>0.2%(符合要求)
因此选项D是正确的。A系根据一侧钢筋最小配筋率计算,B系按照全部纵向钢筋的最小配筋率计算,C纯属计算过程中的错误,都是不正确的。
【点评】:(1)规范7.3.4条指出:当ζ≤ζ
 时为大偏心受压构件,ζ>ζ
时为大偏心受压构件,ζ>ζ 时为小偏心受压构件;由于在计算柱配筋时,A
时为小偏心受压构件;由于在计算柱配筋时,A 和A′
和A′ 均为未知,无从计算ζ,因此不能直接利用上述条件进行判别。
均为未知,无从计算ζ,因此不能直接利用上述条件进行判别。清华大学庄崖屏、叶列平教授(均为《混凝土结构设计规范》(GB50010-2002)第7章正截面承载力计算部分的主要起草人)在规范组组织编写的《混凝土结构设计》一书中给出了如下判别方法。
取界限破坏时的受压区高度x
 =ζ
=ζ h
h 代入大偏心受压的计算公式(即规范公式(7.3.4-1)、(7.3.4-2),并取a=a′,即可得界限破坏时的轴力N
代入大偏心受压的计算公式(即规范公式(7.3.4-1)、(7.3.4-2),并取a=a′,即可得界限破坏时的轴力N 和弯矩M
和弯矩M 如下:
如下:N
 =α
=α f
f bζ
bζ h
h +f′
+f′ A′
A′ -f
-f A
A
M
 =0.5α
=0.5α f
f bζ
bζ h
h (h-ζ
(h-ζ h
h )+0.5(f′
)+0.5(f′ A′
A′ +f
+f A
A )(h
)(h -a)
-a)由此得到相对界限偏心距为:
e
 =M
=M /N
/N h
h =0.5α
=0.5α f
f bζ
bζ h
h (h-ζ
(h-ζ h
h )+0.5(f′
)+0.5(f′ A′
A′ +f
+f A
A )(h
)(h -a)/(α
-a)/(α f
f bζ
bζ h
h +f′
+f′ A′
A′ -f
-f A
A )h
)h
分析上式得知,当构件截面尺寸和材料强度设计值给定,相对界限偏心距e
 b/h
b/h 就取决于截面配筋A
就取决于截面配筋A 与A′
与A′ 。且随A
。且随A 与A′
与A′ 的减小,e
的减小,e b/h
b/h 也随之减小。A
也随之减小。A 与A′
与A′ 取最小配筋率时可得e
取最小配筋率时可得e b/h
b/h 的最小值e
的最小值e /h
/h 。规范规定对偏心受压构件,受拉钢筋A
。规范规定对偏心受压构件,受拉钢筋A 与受压钢筋A′
与受压钢筋A′ 按构件全截面面积计算的最小配筋率均为0.002。并近似取h=1.05h
按构件全截面面积计算的最小配筋率均为0.002。并近似取h=1.05h ,a′=0.05h代入公式(1-11-1),即可得对应于常用的各种混凝土强度等级及HRB335级和HRB400级钢筋,相对界限偏心距的最小值e
,a′=0.05h代入公式(1-11-1),即可得对应于常用的各种混凝土强度等级及HRB335级和HRB400级钢筋,相对界限偏心距的最小值e /h
/h ,即本题开题时所列入的表1-11-1中的对应数值(注:原文对受拉钢筋A
,即本题开题时所列入的表1-11-1中的对应数值(注:原文对受拉钢筋A 按构件全截面面积计算的最小配筋率为0.002和0.45f
按构件全截面面积计算的最小配筋率为0.002和0.45f /f
/f 两者中的较大者,可能系按规范中问稿的规定确定,与正式稿不符,笔者在表1-11-1中已加以改正)。当ηe
两者中的较大者,可能系按规范中问稿的规定确定,与正式稿不符,笔者在表1-11-1中已加以改正)。当ηe ≤e
≤e 时按小偏心受压构件计算;ηe
时按小偏心受压构件计算;ηe >e
>e 时,则应按式(1-11-1)求出e
时,则应按式(1-11-1)求出e /h
/h 后再作出判别。
后再作出判别。对于对称配筋的矩形截面构件,在清华大学滕智明教授主编的《钢筋混凝土基本构件》(第二版)一书中给出了判别方法:
N
 =α
=α f
f bh
bh ζ
ζ
当ηe
 >e
>e ,而ηe
,而ηe ≤e
≤e 且N>N
且N>N 时为小偏心受压构件;当ηe
时为小偏心受压构件;当ηe >e
>e 且N≤N
且N≤N 时为大偏心受压构件。本题即按此求解。
时为大偏心受压构件。本题即按此求解。(2)实际上,我国过去一直采用上述方法判别两种偏心受压情况,但取e
 =0.3h
=0.3h ,那是建立在过去的混凝土强度水平、混凝土采用弯曲抗压强度、钢筋的品种和最小配筋率水平的基础上,现在条件变化了,自然要修改。
,那是建立在过去的混凝土强度水平、混凝土采用弯曲抗压强度、钢筋的品种和最小配筋率水平的基础上,现在条件变化了,自然要修改。