7.偏心受压构件的计算
正确答案:
7.大偏心受压破坏与小偏心受压破坏
(1)概念
对于钢筋混凝土偏心受压短柱,破坏形态有两种:"受拉破坏"与"受压破坏"。
当轴向压力N的相对偏心距较大,且纵向受拉钢筋配置不太多时,靠近轴力一侧受压,另一侧受拉,破坏始于受拉钢筋屈服,以受压区边缘混凝土应变达到极限压应变告终,称作"受拉破坏"。由于通常发生这种破坏对应于相对偏心距较大的情况,故习惯上称作"大偏心受压破坏"。
"受压破坏"则可能发生于以下几种情况:
①N的相对偏心距较小,构件全部受压或大部分受压,截面破坏始于靠近N-侧受压区边缘混凝土应变达到极限压应变,同侧钢筋应力也达到屈服,而离N较远侧钢筋则不能受拉屈服。
②N的相对偏心距很小,且离N较远侧钢筋布置很少时,发生离N较远侧混凝土先被压坏的现象,称"反向破坏"。
③N的相对偏心距虽然较大,但离N较远侧钢筋布置特别多,致使受拉钢筋不屈服,破坏始于靠近N-侧受压区边缘混凝土应变达到极限压应变。
"受压破坏"通常对应于偏心距较小的情况,故习惯上称作"小偏心受压破坏"。
由以上分析可见,发生何种破坏不但与偏心距大小有关,还与截面纵筋的配置数量有关。
(2)大、小偏心的界限
受拉钢筋应力达到屈服强度的同时,受压区边缘混凝土应变达到极限压应变,这种情况称作"界限破坏"。以此区分,当ξ≤ξ 时,为大偏心受压;当ξ>ξ
时,为大偏心受压;当ξ>ξ 时,为小偏心受压。
时,为小偏心受压。
(3)偏心受压构件正截面承载力平衡方程
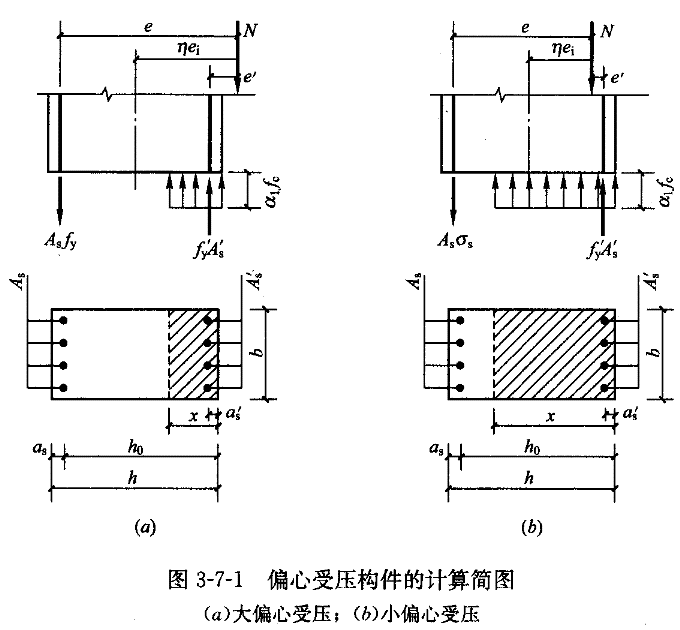
大、小偏心时的计算简图如图3-7-1所示。据此,可以列出平衡方程如下:
大偏心受压时的正截面受压承载力平衡方程为:

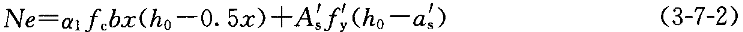

适用条件:
χ≤ξ h
h (3-7-4)
(3-7-4)
z≥2a (3-7-5)
(3-7-5)
小偏心时的正截面受压承载力平衡方程为:
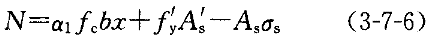
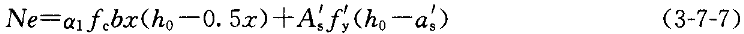
e=ηe +0.5h-a
+0.5h-a (3-7-8)
(3-7-8)
适用条件:
χ>ξ h
h (3-7-9)
(3-7-9)

将σ 与ξ的关系画在坐标上,将更加清楚明了,如图3-7-2所示。
与ξ的关系画在坐标上,将更加清楚明了,如图3-7-2所示。
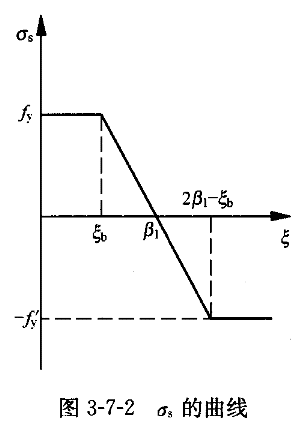
为了下文叙述方便,令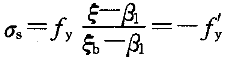 ,将解出的ξ记作ξ
,将解出的ξ记作ξ ,则有ξ
,则有ξ =2β
=2β -ξ
-ξ 。
。
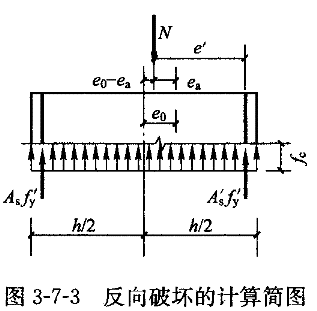
为了防止"反向破坏"(图3-7-3),当N>f A时,应保证满足A
A时,应保证满足A 不能太小,即应满足下式要求:
不能太小,即应满足下式要求:
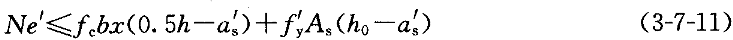

注意,对"反向破坏"验算时,采用e -e
-e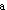 而不是e
而不是e +e
+e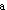 是按照更不利情况考虑的。因为,e
是按照更不利情况考虑的。因为,e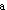 可正可负,当取为负值时,所需要的A
可正可负,当取为负值时,所需要的A 更多。取η=1.0也是同样的考虑。
更多。取η=1.0也是同样的考虑。
2.非对称配筋时的偏心受压构件
(1)配筋设计
如前所述,由于大、小偏心不仅与偏心距有关还与配筋有关,因此,配筋设计时无法利用ξ判断是大偏心还是小偏心,从而影响到平衡方程的选择。
通常,可以这样判断:ηe >0.3h
>0.3h 为大偏心;ηe
为大偏心;ηe ≤0.3h
≤0.3h 为小偏心。之所以用ηe
为小偏心。之所以用ηe 和
和
0.3h 比较判别大、小偏心,见下面的介绍。
比较判别大、小偏心,见下面的介绍。
1)判别公式的由来
根据界限破坏条件,可以建立下面两个平衡方程:


由以上两式可得:
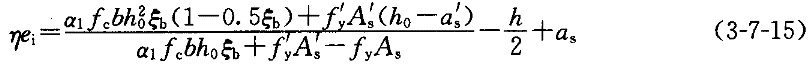
对上式加以整理,得到:
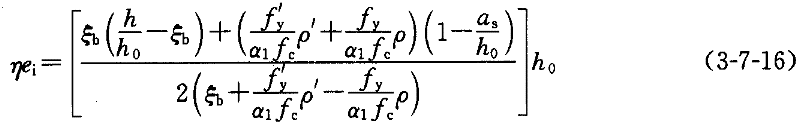
通过分析可知,在式(3-7-16)中,ηe 随配筋率ρ′和ρ′的减小而减小。若取ρ′和ρ为最小值,则ηei
随配筋率ρ′和ρ′的减小而减小。若取ρ′和ρ为最小值,则ηei 必然取得最小值(ηe
必然取得最小值(ηe )min。当实际的ηe
)min。当实际的ηe <(ηe
<(ηe )min时,截面属于小偏心情况。
)min时,截面属于小偏心情况。
若取p'=p=0.2%(0.2%是规范规定的一侧纵向钢筋最小配筋率),h/h =1.05,α
=1.05,α =α
=α =0.05h
=0.05h ,代入式(3-7-16),得到表3-7-1。
,代入式(3-7-16),得到表3-7-1。
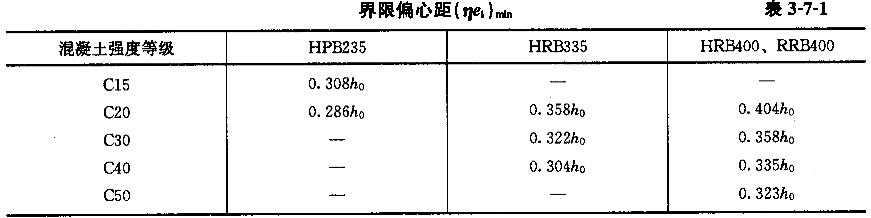
由表可见,(ηe )min在0.3h
)min在0.3h 附近,于是,近似取0.3h
附近,于是,近似取0.3h 作为大、小偏心的界限。
作为大、小偏心的界限。
2)计算步骤
①大偏心情况
当判断为大偏心时,可能有两种情况:
A.A 、A
、A 均未知
均未知
此时,由于三个未知数两个方程,因此应增加一个条件ξ=ξ ,于是方程可解。通常这时的ξ也能使得χ满足χ≥2a
,于是方程可解。通常这时的ξ也能使得χ满足χ≥2a ,故满足全部适用条件。
,故满足全部适用条件。
先依据平衡方程解出A ,公式为:
,公式为:
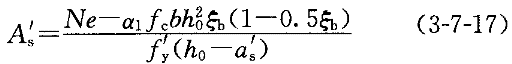
若A 满足一侧最小配筋率,代入下式求解A
满足一侧最小配筋率,代入下式求解A :
:
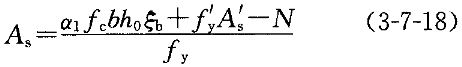
否则,应取A =ρ′
=ρ′ b,然后取定钢筋直径与根数后,按照A
b,然后取定钢筋直径与根数后,按照A 为已知的情况计算。
为已知的情况计算。
B.A 已知,A
已知,A 未知
未知
此时,两个未知数,两个方程,可解。若A 满足一侧最小配筋率取值,先求出χ,χ可能出现下列情况:
满足一侧最小配筋率取值,先求出χ,χ可能出现下列情况:
a.满足χ≤ξ h
h 且χ≥2a
且χ≥2a 的适用条件,于是
的适用条件,于是
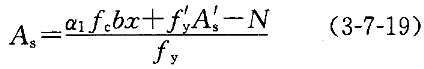
b.若χ<2a ,则取χ=2a
,则取χ=2a ,然后对A
,然后对A 合力点位置取矩,求出A
合力点位置取矩,求出A 。公式为
。公式为
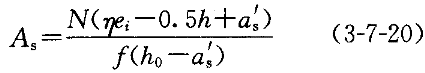
另外,再按照不考虑A ,即取A
,即取A =0求算A
=0求算A ,取二者的较小者。
,取二者的较小者。
c.若χ>ξ h
h ,则表明A'配置不足,需要按照A
,则表明A'配置不足,需要按照A 未知的情况计算;或加大截面。
未知的情况计算;或加大截面。
以上计算中,A 应满足一侧纵筋最小配筋率的要求,A
应满足一侧纵筋最小配筋率的要求,A +A
+A 应满足全部纵筋最小配筋率要求。
应满足全部纵筋最小配筋率要求。
②小偏心情况
当判断为小偏心时,由于A 应力通常较小,通常可按最小配筋率取值,即A
应力通常较小,通常可按最小配筋率取值,即A =ρ′
=ρ′ bh=0.002bh。考虑到A
bh=0.002bh。考虑到A 过少可能引起"反向破坏",因此,当N>f
过少可能引起"反向破坏",因此,当N>f A时,A
A时,A 尚应满足下式要求(混凝土规范7.3.4条第3款):
尚应满足下式要求(混凝土规范7.3.4条第3款):
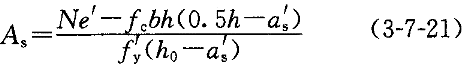
e′=0.5h-a (e
(e -e
-e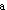 )(3-7-22)
)(3-7-22)
即,As应该取0.002bh和上式的较大者。取定A 后,方程可解。利用小偏心时的平衡方程求出χ,ξ=χ/h
后,方程可解。利用小偏心时的平衡方程求出χ,ξ=χ/h ,ξ可能出现以下情况:
,ξ可能出现以下情况:
a.ξ <ξ<ξ
<ξ<ξ
表明A 未达到屈服,σ
未达到屈服,σ 在f
在f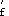 和f
和f 之间,原来代入基本公式的
之间,原来代入基本公式的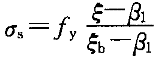 是合适的,满足适用条件,将ξ代入公式求出另一个未知数A
是合适的,满足适用条件,将ξ代入公式求出另一个未知数A 。
。
b.ξ ≤ξ<h/h
≤ξ<h/h
此时A 受压屈服,取σ
受压屈服,取σ =-f
=-f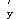 ,基本公式转化为下式:
,基本公式转化为下式:
N=α f
f b
b  +f
+f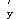 A
A +f
+f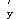 A
A (3-7-23)
(3-7-23)
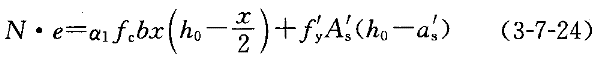
e=ηe +0.5h-a
+0.5h-a (3-7-25)
(3-7-25)
重新求解χ和A 。
。
c.ξ≥h/h ,且ξ>ξ
,且ξ>ξ
表示A 受压屈服,且中和轴已经在截面之外,于是,取σ
受压屈服,且中和轴已经在截面之外,于是,取σ =-f
=-f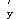 ,χ=h,α
,χ=h,α =1,代入基本公式直接解得A
=1,代入基本公式直接解得A :
:
 s
s
以上计算得到的A 应满足一侧纵筋最小配筋率,A
应满足一侧纵筋最小配筋率,A +A
+A 应满足全部纵筋配筋率的要求。
应满足全部纵筋配筋率的要求。
(2)承载力复核
偏心受压柱截面承载力复核应包括两个方面:弯矩作用平面和垂直于弯矩作用平面,承载力应取二者的较小者。垂直于弯矩作用平面按照轴心受压构件考虑,比较简单,这里只介绍弯矩作用平面的计算。
1)给定偏心距e ,求轴力设计值N
,求轴力设计值N
由于N未知,所以无法计算出ζ ,也就无法得到η的值。可假定ζ
,也就无法得到η的值。可假定ζ =1.0,待求出N之后再进行验证。
=1.0,待求出N之后再进行验证。
按照大偏心受压的计算简图(更准确无误的说,应是界限破坏的计算简图,这样在概念上更不容易迷惑,只不过是界限破坏也算作大偏心破坏),对轴向力N作用位置取矩(可参照图3-7-1a理解),公式为:
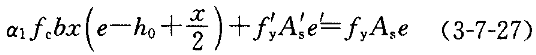
解方程求出χ,可能有以下几种情况:
①若χ≤ξbh 且χ≥2a
且χ≥2a ,则满足大偏心受压的适用条件,根据轴向力的平衡方程求出N。
,则满足大偏心受压的适用条件,根据轴向力的平衡方程求出N。
②若χ≤ξ h
h 且χ<2a
且χ<2a ,则取χ=2a
,则取χ=2a ,按照大偏心受压对A
,按照大偏心受压对A 合力点位置取矩求出N。
合力点位置取矩求出N。
由于平衡方程成立的前提条件是χ≤ξ h
h ,故当解出χ≤ξ
,故当解出χ≤ξ h
h 时表明原来的假定无误,χ值是可以接受的。否则,解出的χ变得无意义。
时表明原来的假定无误,χ值是可以接受的。否则,解出的χ变得无意义。
③当χ>ξ h
h 时,属于小偏心,应以
时,属于小偏心,应以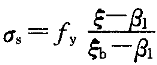 代入小偏心平衡公式,重新求解χ。得到的ξ可能出现下面的情况:
代入小偏心平衡公式,重新求解χ。得到的ξ可能出现下面的情况:
a.ξ <ξ<ξ,满足小偏心的适用条件,将ξ代入小偏心的平衡公式求解N。
<ξ<ξ,满足小偏心的适用条件,将ξ代入小偏心的平衡公式求解N。
b.ξ ≤ξ<h/h
≤ξ<h/h ,此时A
,此时A 受压屈服,取σ
受压屈服,取σ =-f
=-f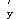 A
A ,基本公式转化为下式:
,基本公式转化为下式:
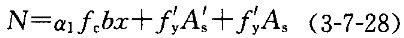
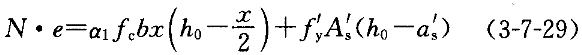
e=ηe +0.5h-a
+0.5h-a (3-7-30)
(3-7-30)
重新求解χ,计算N。
c.ξ≥h/h 且ξ>ξ
且ξ>ξ ,表示A
,表示A 受压屈服,且中和轴已经在截面之外,于是,取σ
受压屈服,且中和轴已经在截面之外,于是,取σ =-f
=-f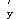 ,χ=h,α
,χ=h,α =1,代入小偏心的基本公式解出N。
=1,代入小偏心的基本公式解出N。
2)给定轴力设计值N,求弯矩作用平面的弯矩设计值M
因为M=N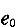 ,所以,这里的关键是求出e
,所以,这里的关键是求出e ,而求出ηe
,而求出ηe 则可以求出e
则可以求出e 进而得到e
进而得到e ,所采用的公式如下:
,所采用的公式如下:
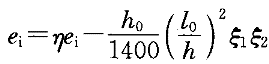
e =e
=e -e
-e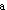
依据大偏心受压列出平衡方程,此时,未知数只有χ和ηe 两个,利用下式解出χ:
两个,利用下式解出χ:
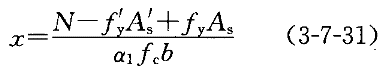
χ可能出现以下情况:
①当χ≤ξ h
h ,且χ≥2a
,且χ≥2a 时,满足大偏心受压的适用条件,将解出的χ代入大偏心受压的平衡方程求出ηe
时,满足大偏心受压的适用条件,将解出的χ代入大偏心受压的平衡方程求出ηe 。
。
②当χ≤ξ h
h 且χ<2a
且χ<2a 时,取χ=2a
时,取χ=2a ,对A
,对A 合力点位置取矩,得到
合力点位置取矩,得到
Ne′=A f
f (h
(h -a
-a )(3-7-32)
)(3-7-32)
计算出e′后进而可以得到ηe 。
。
③当χ>ξ h
h 时,属于小偏心,应以
时,属于小偏心,应以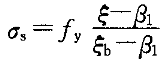 代入小偏心平衡公式,重新求解χ。得到的ξ可能出现下面的情况:
代入小偏心平衡公式,重新求解χ。得到的ξ可能出现下面的情况:
a.ξ <ξ<ξ
<ξ<ξ =(2β-ξ
=(2β-ξ ),满足小偏心的适用条件,将ξ代入小偏心的平衡公式求解ηe
),满足小偏心的适用条件,将ξ代入小偏心的平衡公式求解ηe 。
。
b.ξ ≤ξ<h/h
≤ξ<h/h ,此时A
,此时A 受压屈服,取σ
受压屈服,取σ =-f
=-f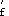 ,基本公式转化为下式:
,基本公式转化为下式:
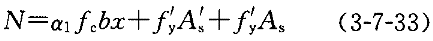
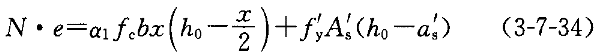
e=ηe +0.5h-a
+0.5h-a (3-7-35)
(3-7-35)
重新求解χ,进而求出ηe 。
。
c.ξ≥h/h 且ξ
且ξ ,表示A
,表示A 受压屈服,且中和轴已经在截面之外,于是,取σ
受压屈服,且中和轴已经在截面之外,于是,取σ =-f
=-f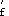 ,χ=h,α
,χ=h,α =1,代入小偏心的基本公式解出ηe
=1,代入小偏心的基本公式解出ηe 。
。
对于小偏心受压的情况,当N>f A时,尚需要验算"反向破坏",弯矩作用平面的承载力应取正向破坏和反向破坏的较小者。
A时,尚需要验算"反向破坏",弯矩作用平面的承载力应取正向破坏和反向破坏的较小者。
3.对称配筋时的偏向受压构件
矩形截面偏心受压柱,若采用对称配筋,在截面设计时如何区分大、小偏心,目前有两种观点:
(1)滕智明《钢筋混凝土基本构件》(清华大学出版社,1987)一书中指出,ηe >0.3h
>0.3h 且χ≤ξ
且χ≤ξ h
h 时为大偏心受压;ηe
时为大偏心受压;ηe ≤0.3h
≤0.3h ,或ηe
,或ηe >0.3h
>0.3h 且χ>ξ
且χ>ξ h
h 时为小偏心受压。持此观点的还有:舒士霖《钢筋混凝土结构》(第二版,浙江大学出版社,2003);沈蒲生《混凝土结构设计原理》(第三版,高等教育出版社,2005);沙志国《-级注册结构工程师模拟试题与解答点评》(第二版,中国建筑工业出版社,2010)(该书第28页"当ηe
时为小偏心受压。持此观点的还有:舒士霖《钢筋混凝土结构》(第二版,浙江大学出版社,2003);沈蒲生《混凝土结构设计原理》(第三版,高等教育出版社,2005);沙志国《-级注册结构工程师模拟试题与解答点评》(第二版,中国建筑工业出版社,2010)(该书第28页"当ηe >e
>e ,或ηe
,或ηe ≤e
≤e 且N>N
且N>N 时为小偏心受压构件;当ηe
时为小偏心受压构件;当ηe >e
>e 且N≤N
且N≤N 时为大偏心受压构件",笔者认为应是作者的笔误,其原意应是"当ηe
时为大偏心受压构件",笔者认为应是作者的笔误,其原意应是"当ηe ≤e
≤e ,或ηe
,或ηe >e
>e 且N>N
且N>N 时为小偏心受压构件;当ηe
时为小偏心受压构件;当ηe >e
>e 且N≤N
且N≤N 时为大偏心受压构件。")等。
时为大偏心受压构件。")等。
(2)施岚青《一、二级注册结构工程师专业考试应试指南》(中国建筑工业出版社,2008)认为,直接根据受压区高度判断,即,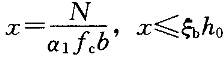 时为大偏心,χ>ξ
时为大偏心,χ>ξ h
h 时为小偏心。
时为小偏心。
三校合编《混凝土结构》(上册,第四版,中国建筑工业出版社,2009)一书未明确说明。
笔者认为,观点(1)值得商榷。下面以一个算例说明。
已知一矩形截面钢筋混凝土柱,截面尺寸b×h=400mm×600mm,柱的计算长度为6m。在控制截面上有轴心压力设计值N=1000kN,弯矩设计值M=85kN.m。混凝土强度等级C30,纵向受力钢筋为HRB400。要求计算纵筋截面积A =A
=A 。
。
解:取a =a
=a =40mm,则h
=40mm,则h =560mm。容易求得e
=560mm。容易求得e =105mm,η=1.381。
=105mm,η=1.381。
于是,按照观点(1)计算如下:
ηe =1.381×105=145mm<0.3h
=1.381×105=145mm<0.3h =0.3×560-203mm按小偏心受压计算。
=0.3×560-203mm按小偏心受压计算。
依据《混凝土结构设计规范》GB50010-2002的7.3.4条第4款列出的公式求ξ,如下:
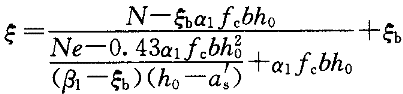
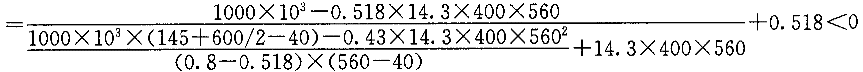
出现ξ为负值的情况,显然不合理,若用此ξ值代入混凝土规范公式7.3.4-7计算A ,A
,A 必然导致结果过大。若取ξ=0,则可得
必然导致结果过大。若取ξ=0,则可得
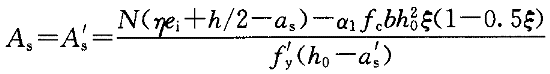

下面再采用观点(2)计算如下:
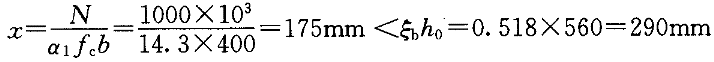
按照大偏心进行计算。于是

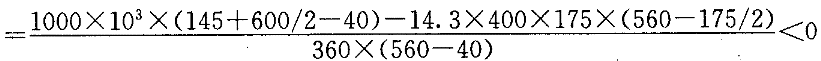
说明只需要按照构造要求配筋。
根据混凝土规范的9.5.1条,受压构件全部纵向钢筋最小配筋率为0.6%,一侧纵向钢筋最小配筋率为0.2%,由于采用HRB400钢筋,全部纵向钢筋最小配筋率减小为0.5%。于是一侧钢筋配筋率为0.25%,即A =A
=A =0.25%×400×600=600mm
=0.25%×400×600=600mm 。
。
那么,取A =A
=A =600mm
=600mm ,a
,a =a
=a =40mm,是否满足承载力要求呢?
=40mm,是否满足承载力要求呢?
今按照已知N求M对承载力进行复核如下。
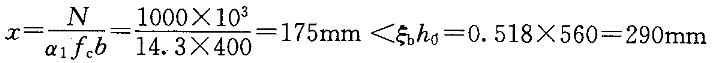
按照大偏心受压考虑。

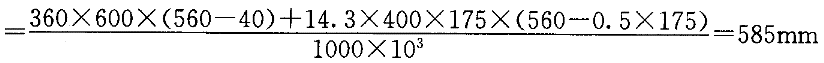
根据e与ηe ,的关系,可知
,的关系,可知
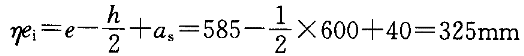
由于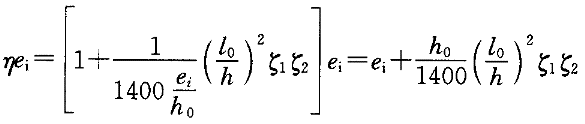
故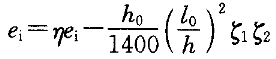
今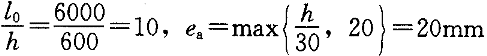 。
。
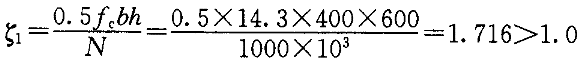 ,取ξ
,取ξ =1.0
=1.0
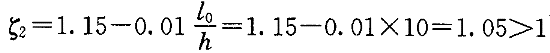 ,取ξ
,取ξ =1.0
=1.0
于是可以解出: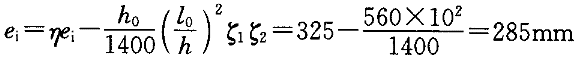
e =e
=e -e
-e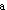 =285-20=265mm
=285-20=265mm
截面h方向可承受的弯矩为
M =Ne
=Ne =1000×0.265=265kN.m>85kN.m
=1000×0.265=265kN.m>85kN.m
可见,承载力满足要求。
综上可见,对称配筋偏心受压构件当计算所需纵向钢筋截面积时,步骤为:
(1)计算混凝土相对受压区高度:
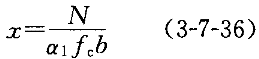
(2)若满足适用条件χ≤ξ h
h 且χ≥2a
且χ≥2a ,则利用下式计算配筋量:
,则利用下式计算配筋量:
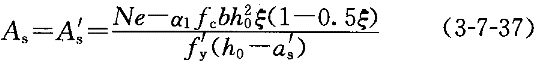
若χ≤ξ h
h 但χ<2a
但χ<2a ,此时受压钢筋A
,此时受压钢筋A 没有屈服。取χ=2a
没有屈服。取χ=2a ,然后对A
,然后对A 合力点取矩,得到
合力点取矩,得到
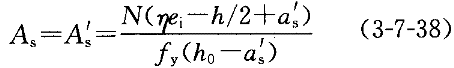
(3)若χ>ξ h
h ,利用下式先求出ξ,然后再计算A
,利用下式先求出ξ,然后再计算A =A
=A 。
。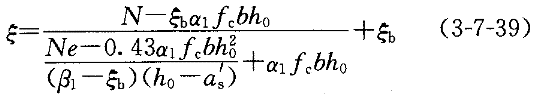
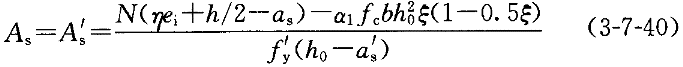
4.总结
笔者将偏心受压构件的内容归纳如下:
(1)最好不要采用"大偏心受压构件"、"小偏心受压构件"这样的称谓,因为容易产生误解,以为构件本身是"大偏心受压构件"或者"小偏心受压构件"。实际上,大、小偏心只是两种破坏形式的通俗称呼,而且并不规范。ArthurH.Nilson在其名著《DesignofConcreteStructures》-书中,将破坏类型称作"tension-controlledfailure"(受拉控制的破坏)、"compression-controlledfailure"(受压控制的破坏),笔者认为更恰当。 (2)大、小偏心破坏并不只是与偏心距有关,还与轴向力的大小以及配筋情况有关。
(3)矩形截面偏心受压柱,若采用对称配筋,在截面设计时,直接利用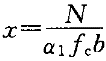 判别大小偏心。
判别大小偏心。
(4)偏心受压构件的计算看起来公式很长,步骤很多,其本质,只不过是依据计算简图建立平衡方程然后解方程而已(由于《混凝土结构设计规范》GB50010-2002规定了σ 的线性简化计算公式,因此最多只是解一元二次方程;《公路钢筋混凝土及预应力混凝土桥涵设计规范》JTGD62-2004中未规定σ
的线性简化计算公式,因此最多只是解一元二次方程;《公路钢筋混凝土及预应力混凝土桥涵设计规范》JTGD62-2004中未规定σ 的简化计算公式,会出现解一元三次方程的情况)。
的简化计算公式,会出现解一元三次方程的情况)。
(5)平衡方程依据力的平衡和弯矩的平衡建立,独立方程只有两个。适用条件是为了保证平衡方程的正确性。χ≤ξ h
h 是为了保证A
是为了保证A f
f 的正确性;χ≥2a
的正确性;χ≥2a 是为了保证f
是为了保证f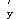 A
A 的正确性;
的正确性;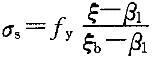 只有在-f
只有在-f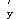 和f
和f 之间才是正确的。
之间才是正确的。
(1)概念
对于钢筋混凝土偏心受压短柱,破坏形态有两种:"受拉破坏"与"受压破坏"。
当轴向压力N的相对偏心距较大,且纵向受拉钢筋配置不太多时,靠近轴力一侧受压,另一侧受拉,破坏始于受拉钢筋屈服,以受压区边缘混凝土应变达到极限压应变告终,称作"受拉破坏"。由于通常发生这种破坏对应于相对偏心距较大的情况,故习惯上称作"大偏心受压破坏"。
"受压破坏"则可能发生于以下几种情况:
①N的相对偏心距较小,构件全部受压或大部分受压,截面破坏始于靠近N-侧受压区边缘混凝土应变达到极限压应变,同侧钢筋应力也达到屈服,而离N较远侧钢筋则不能受拉屈服。
②N的相对偏心距很小,且离N较远侧钢筋布置很少时,发生离N较远侧混凝土先被压坏的现象,称"反向破坏"。
③N的相对偏心距虽然较大,但离N较远侧钢筋布置特别多,致使受拉钢筋不屈服,破坏始于靠近N-侧受压区边缘混凝土应变达到极限压应变。
"受压破坏"通常对应于偏心距较小的情况,故习惯上称作"小偏心受压破坏"。
由以上分析可见,发生何种破坏不但与偏心距大小有关,还与截面纵筋的配置数量有关。
(2)大、小偏心的界限
受拉钢筋应力达到屈服强度的同时,受压区边缘混凝土应变达到极限压应变,这种情况称作"界限破坏"。以此区分,当ξ≤ξ
 时,为大偏心受压;当ξ>ξ
时,为大偏心受压;当ξ>ξ 时,为小偏心受压。
时,为小偏心受压。(3)偏心受压构件正截面承载力平衡方程
大、小偏心时的计算简图如图3-7-1所示。据此,可以列出平衡方程如下:
大偏心受压时的正截面受压承载力平衡方程为:

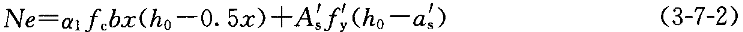

适用条件:
χ≤ξ
 h
h (3-7-4)
(3-7-4)z≥2a
 (3-7-5)
(3-7-5)小偏心时的正截面受压承载力平衡方程为:

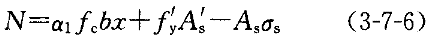
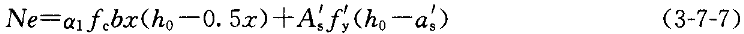
e=ηe
 +0.5h-a
+0.5h-a (3-7-8)
(3-7-8)适用条件:
χ>ξ
 h
h (3-7-9)
(3-7-9)
将σ
 与ξ的关系画在坐标上,将更加清楚明了,如图3-7-2所示。
与ξ的关系画在坐标上,将更加清楚明了,如图3-7-2所示。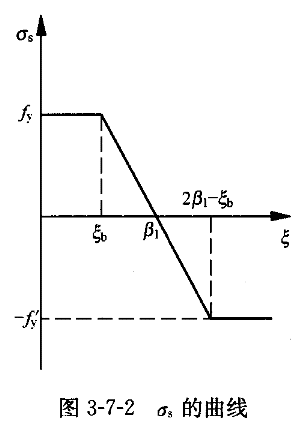
为了下文叙述方便,令
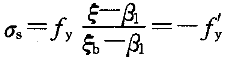 ,将解出的ξ记作ξ
,将解出的ξ记作ξ ,则有ξ
,则有ξ =2β
=2β -ξ
-ξ 。
。为了防止"反向破坏"(图3-7-3),当N>f
 A时,应保证满足A
A时,应保证满足A 不能太小,即应满足下式要求:
不能太小,即应满足下式要求:
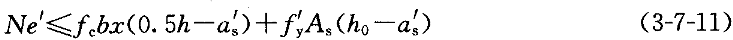

注意,对"反向破坏"验算时,采用e
 -e
-e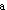 而不是e
而不是e +e
+e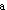 是按照更不利情况考虑的。因为,e
是按照更不利情况考虑的。因为,e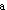 可正可负,当取为负值时,所需要的A
可正可负,当取为负值时,所需要的A 更多。取η=1.0也是同样的考虑。
更多。取η=1.0也是同样的考虑。2.非对称配筋时的偏心受压构件
(1)配筋设计
如前所述,由于大、小偏心不仅与偏心距有关还与配筋有关,因此,配筋设计时无法利用ξ判断是大偏心还是小偏心,从而影响到平衡方程的选择。
通常,可以这样判断:ηe
 >0.3h
>0.3h 为大偏心;ηe
为大偏心;ηe ≤0.3h
≤0.3h 为小偏心。之所以用ηe
为小偏心。之所以用ηe 和
和0.3h
 比较判别大、小偏心,见下面的介绍。
比较判别大、小偏心,见下面的介绍。1)判别公式的由来
根据界限破坏条件,可以建立下面两个平衡方程:


由以上两式可得:
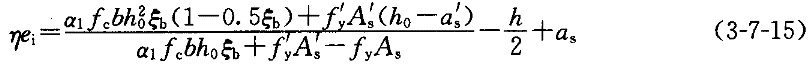
对上式加以整理,得到:
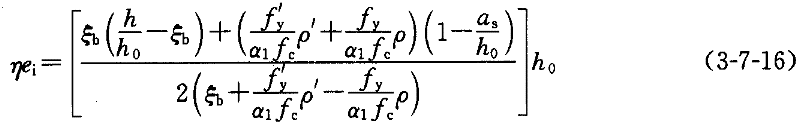
通过分析可知,在式(3-7-16)中,ηe
 随配筋率ρ′和ρ′的减小而减小。若取ρ′和ρ为最小值,则ηei
随配筋率ρ′和ρ′的减小而减小。若取ρ′和ρ为最小值,则ηei 必然取得最小值(ηe
必然取得最小值(ηe )min。当实际的ηe
)min。当实际的ηe <(ηe
<(ηe )min时,截面属于小偏心情况。
)min时,截面属于小偏心情况。若取p'=p=0.2%(0.2%是规范规定的一侧纵向钢筋最小配筋率),h/h
 =1.05,α
=1.05,α =α
=α =0.05h
=0.05h ,代入式(3-7-16),得到表3-7-1。
,代入式(3-7-16),得到表3-7-1。
由表可见,(ηe
 )min在0.3h
)min在0.3h 附近,于是,近似取0.3h
附近,于是,近似取0.3h 作为大、小偏心的界限。
作为大、小偏心的界限。2)计算步骤
①大偏心情况
当判断为大偏心时,可能有两种情况:
A.A
 、A
、A 均未知
均未知此时,由于三个未知数两个方程,因此应增加一个条件ξ=ξ
 ,于是方程可解。通常这时的ξ也能使得χ满足χ≥2a
,于是方程可解。通常这时的ξ也能使得χ满足χ≥2a ,故满足全部适用条件。
,故满足全部适用条件。先依据平衡方程解出A
 ,公式为:
,公式为: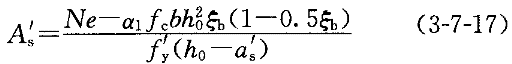
若A
 满足一侧最小配筋率,代入下式求解A
满足一侧最小配筋率,代入下式求解A :
: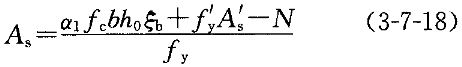
否则,应取A
 =ρ′
=ρ′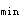 b,然后取定钢筋直径与根数后,按照A
b,然后取定钢筋直径与根数后,按照A 为已知的情况计算。
为已知的情况计算。B.A
 已知,A
已知,A 未知
未知此时,两个未知数,两个方程,可解。若A
 满足一侧最小配筋率取值,先求出χ,χ可能出现下列情况:
满足一侧最小配筋率取值,先求出χ,χ可能出现下列情况:a.满足χ≤ξ
 h
h 且χ≥2a
且χ≥2a 的适用条件,于是
的适用条件,于是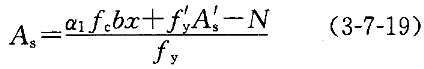
b.若χ<2a
 ,则取χ=2a
,则取χ=2a ,然后对A
,然后对A 合力点位置取矩,求出A
合力点位置取矩,求出A 。公式为
。公式为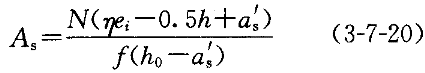
另外,再按照不考虑A
 ,即取A
,即取A =0求算A
=0求算A ,取二者的较小者。
,取二者的较小者。c.若χ>ξ
 h
h ,则表明A'配置不足,需要按照A
,则表明A'配置不足,需要按照A 未知的情况计算;或加大截面。
未知的情况计算;或加大截面。以上计算中,A
 应满足一侧纵筋最小配筋率的要求,A
应满足一侧纵筋最小配筋率的要求,A +A
+A 应满足全部纵筋最小配筋率要求。
应满足全部纵筋最小配筋率要求。②小偏心情况
当判断为小偏心时,由于A
 应力通常较小,通常可按最小配筋率取值,即A
应力通常较小,通常可按最小配筋率取值,即A =ρ′
=ρ′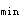 bh=0.002bh。考虑到A
bh=0.002bh。考虑到A 过少可能引起"反向破坏",因此,当N>f
过少可能引起"反向破坏",因此,当N>f A时,A
A时,A 尚应满足下式要求(混凝土规范7.3.4条第3款):
尚应满足下式要求(混凝土规范7.3.4条第3款):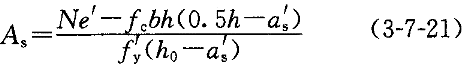
e′=0.5h-a
 (e
(e -e
-e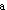 )(3-7-22)
)(3-7-22)即,As应该取0.002bh和上式的较大者。取定A
 后,方程可解。利用小偏心时的平衡方程求出χ,ξ=χ/h
后,方程可解。利用小偏心时的平衡方程求出χ,ξ=χ/h ,ξ可能出现以下情况:
,ξ可能出现以下情况:a.ξ
 <ξ<ξ
<ξ<ξ
表明A
 未达到屈服,σ
未达到屈服,σ 在f
在f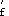 和f
和f 之间,原来代入基本公式的
之间,原来代入基本公式的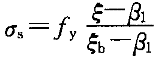 是合适的,满足适用条件,将ξ代入公式求出另一个未知数A
是合适的,满足适用条件,将ξ代入公式求出另一个未知数A 。
。b.ξ
 ≤ξ<h/h
≤ξ<h/h
此时A
 受压屈服,取σ
受压屈服,取σ =-f
=-f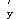 ,基本公式转化为下式:
,基本公式转化为下式:N=α
 f
f b
b  +f
+f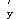 A
A +f
+f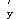 A
A (3-7-23)
(3-7-23)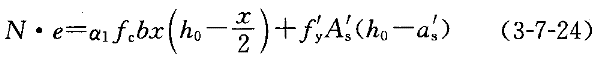
e=ηe
 +0.5h-a
+0.5h-a (3-7-25)
(3-7-25)重新求解χ和A
 。
。c.ξ≥h/h
 ,且ξ>ξ
,且ξ>ξ
表示A
 受压屈服,且中和轴已经在截面之外,于是,取σ
受压屈服,且中和轴已经在截面之外,于是,取σ =-f
=-f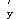 ,χ=h,α
,χ=h,α =1,代入基本公式直接解得A
=1,代入基本公式直接解得A :
: s
s以上计算得到的A
 应满足一侧纵筋最小配筋率,A
应满足一侧纵筋最小配筋率,A +A
+A 应满足全部纵筋配筋率的要求。
应满足全部纵筋配筋率的要求。(2)承载力复核
偏心受压柱截面承载力复核应包括两个方面:弯矩作用平面和垂直于弯矩作用平面,承载力应取二者的较小者。垂直于弯矩作用平面按照轴心受压构件考虑,比较简单,这里只介绍弯矩作用平面的计算。
1)给定偏心距e
 ,求轴力设计值N
,求轴力设计值N由于N未知,所以无法计算出ζ
 ,也就无法得到η的值。可假定ζ
,也就无法得到η的值。可假定ζ =1.0,待求出N之后再进行验证。
=1.0,待求出N之后再进行验证。按照大偏心受压的计算简图(更准确无误的说,应是界限破坏的计算简图,这样在概念上更不容易迷惑,只不过是界限破坏也算作大偏心破坏),对轴向力N作用位置取矩(可参照图3-7-1a理解),公式为:
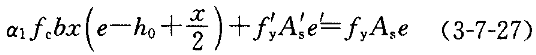
解方程求出χ,可能有以下几种情况:
①若χ≤ξbh
 且χ≥2a
且χ≥2a ,则满足大偏心受压的适用条件,根据轴向力的平衡方程求出N。
,则满足大偏心受压的适用条件,根据轴向力的平衡方程求出N。②若χ≤ξ
 h
h 且χ<2a
且χ<2a ,则取χ=2a
,则取χ=2a ,按照大偏心受压对A
,按照大偏心受压对A 合力点位置取矩求出N。
合力点位置取矩求出N。由于平衡方程成立的前提条件是χ≤ξ
 h
h ,故当解出χ≤ξ
,故当解出χ≤ξ h
h 时表明原来的假定无误,χ值是可以接受的。否则,解出的χ变得无意义。
时表明原来的假定无误,χ值是可以接受的。否则,解出的χ变得无意义。③当χ>ξ
 h
h 时,属于小偏心,应以
时,属于小偏心,应以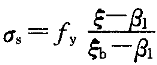 代入小偏心平衡公式,重新求解χ。得到的ξ可能出现下面的情况:
代入小偏心平衡公式,重新求解χ。得到的ξ可能出现下面的情况:a.ξ
 <ξ<ξ,满足小偏心的适用条件,将ξ代入小偏心的平衡公式求解N。
<ξ<ξ,满足小偏心的适用条件,将ξ代入小偏心的平衡公式求解N。b.ξ
 ≤ξ<h/h
≤ξ<h/h ,此时A
,此时A 受压屈服,取σ
受压屈服,取σ =-f
=-f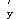 A
A ,基本公式转化为下式:
,基本公式转化为下式: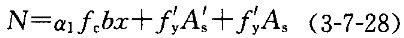
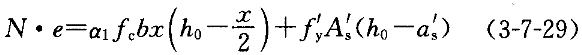
e=ηe
 +0.5h-a
+0.5h-a (3-7-30)
(3-7-30)重新求解χ,计算N。
c.ξ≥h/h
 且ξ>ξ
且ξ>ξ ,表示A
,表示A 受压屈服,且中和轴已经在截面之外,于是,取σ
受压屈服,且中和轴已经在截面之外,于是,取σ =-f
=-f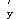 ,χ=h,α
,χ=h,α =1,代入小偏心的基本公式解出N。
=1,代入小偏心的基本公式解出N。2)给定轴力设计值N,求弯矩作用平面的弯矩设计值M
因为M=N
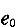 ,所以,这里的关键是求出e
,所以,这里的关键是求出e ,而求出ηe
,而求出ηe 则可以求出e
则可以求出e 进而得到e
进而得到e ,所采用的公式如下:
,所采用的公式如下: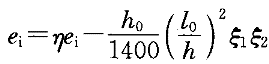
e
 =e
=e -e
-e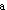
依据大偏心受压列出平衡方程,此时,未知数只有χ和ηe
 两个,利用下式解出χ:
两个,利用下式解出χ: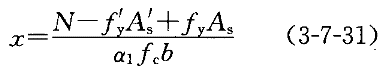
χ可能出现以下情况:
①当χ≤ξ
 h
h ,且χ≥2a
,且χ≥2a 时,满足大偏心受压的适用条件,将解出的χ代入大偏心受压的平衡方程求出ηe
时,满足大偏心受压的适用条件,将解出的χ代入大偏心受压的平衡方程求出ηe 。
。②当χ≤ξ
 h
h 且χ<2a
且χ<2a 时,取χ=2a
时,取χ=2a ,对A
,对A 合力点位置取矩,得到
合力点位置取矩,得到Ne′=A
 f
f (h
(h -a
-a )(3-7-32)
)(3-7-32)计算出e′后进而可以得到ηe
 。
。③当χ>ξ
 h
h 时,属于小偏心,应以
时,属于小偏心,应以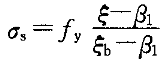 代入小偏心平衡公式,重新求解χ。得到的ξ可能出现下面的情况:
代入小偏心平衡公式,重新求解χ。得到的ξ可能出现下面的情况:a.ξ
 <ξ<ξ
<ξ<ξ =(2β-ξ
=(2β-ξ ),满足小偏心的适用条件,将ξ代入小偏心的平衡公式求解ηe
),满足小偏心的适用条件,将ξ代入小偏心的平衡公式求解ηe 。
。b.ξ
 ≤ξ<h/h
≤ξ<h/h ,此时A
,此时A 受压屈服,取σ
受压屈服,取σ =-f
=-f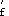 ,基本公式转化为下式:
,基本公式转化为下式: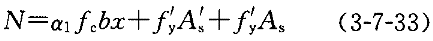
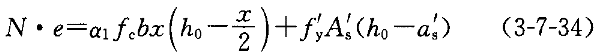
e=ηe
 +0.5h-a
+0.5h-a (3-7-35)
(3-7-35)重新求解χ,进而求出ηe
 。
。c.ξ≥h/h
 且ξ
且ξ ,表示A
,表示A 受压屈服,且中和轴已经在截面之外,于是,取σ
受压屈服,且中和轴已经在截面之外,于是,取σ =-f
=-f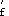 ,χ=h,α
,χ=h,α =1,代入小偏心的基本公式解出ηe
=1,代入小偏心的基本公式解出ηe 。
。对于小偏心受压的情况,当N>f
 A时,尚需要验算"反向破坏",弯矩作用平面的承载力应取正向破坏和反向破坏的较小者。
A时,尚需要验算"反向破坏",弯矩作用平面的承载力应取正向破坏和反向破坏的较小者。3.对称配筋时的偏向受压构件
矩形截面偏心受压柱,若采用对称配筋,在截面设计时如何区分大、小偏心,目前有两种观点:
(1)滕智明《钢筋混凝土基本构件》(清华大学出版社,1987)一书中指出,ηe
 >0.3h
>0.3h 且χ≤ξ
且χ≤ξ h
h 时为大偏心受压;ηe
时为大偏心受压;ηe ≤0.3h
≤0.3h ,或ηe
,或ηe >0.3h
>0.3h 且χ>ξ
且χ>ξ h
h 时为小偏心受压。持此观点的还有:舒士霖《钢筋混凝土结构》(第二版,浙江大学出版社,2003);沈蒲生《混凝土结构设计原理》(第三版,高等教育出版社,2005);沙志国《-级注册结构工程师模拟试题与解答点评》(第二版,中国建筑工业出版社,2010)(该书第28页"当ηe
时为小偏心受压。持此观点的还有:舒士霖《钢筋混凝土结构》(第二版,浙江大学出版社,2003);沈蒲生《混凝土结构设计原理》(第三版,高等教育出版社,2005);沙志国《-级注册结构工程师模拟试题与解答点评》(第二版,中国建筑工业出版社,2010)(该书第28页"当ηe >e
>e ,或ηe
,或ηe ≤e
≤e 且N>N
且N>N 时为小偏心受压构件;当ηe
时为小偏心受压构件;当ηe >e
>e 且N≤N
且N≤N 时为大偏心受压构件",笔者认为应是作者的笔误,其原意应是"当ηe
时为大偏心受压构件",笔者认为应是作者的笔误,其原意应是"当ηe ≤e
≤e ,或ηe
,或ηe >e
>e 且N>N
且N>N 时为小偏心受压构件;当ηe
时为小偏心受压构件;当ηe >e
>e 且N≤N
且N≤N 时为大偏心受压构件。")等。
时为大偏心受压构件。")等。(2)施岚青《一、二级注册结构工程师专业考试应试指南》(中国建筑工业出版社,2008)认为,直接根据受压区高度判断,即,
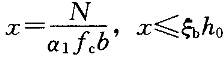 时为大偏心,χ>ξ
时为大偏心,χ>ξ h
h 时为小偏心。
时为小偏心。三校合编《混凝土结构》(上册,第四版,中国建筑工业出版社,2009)一书未明确说明。
笔者认为,观点(1)值得商榷。下面以一个算例说明。
已知一矩形截面钢筋混凝土柱,截面尺寸b×h=400mm×600mm,柱的计算长度为6m。在控制截面上有轴心压力设计值N=1000kN,弯矩设计值M=85kN.m。混凝土强度等级C30,纵向受力钢筋为HRB400。要求计算纵筋截面积A
 =A
=A 。
。解:取a
 =a
=a =40mm,则h
=40mm,则h =560mm。容易求得e
=560mm。容易求得e =105mm,η=1.381。
=105mm,η=1.381。于是,按照观点(1)计算如下:
ηe
 =1.381×105=145mm<0.3h
=1.381×105=145mm<0.3h =0.3×560-203mm按小偏心受压计算。
=0.3×560-203mm按小偏心受压计算。依据《混凝土结构设计规范》GB50010-2002的7.3.4条第4款列出的公式求ξ,如下:
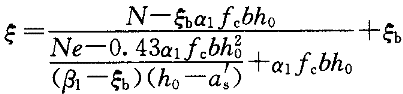
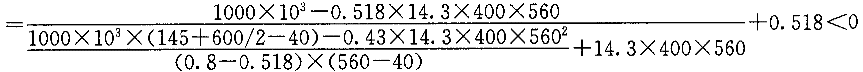
出现ξ为负值的情况,显然不合理,若用此ξ值代入混凝土规范公式7.3.4-7计算A
 ,A
,A 必然导致结果过大。若取ξ=0,则可得
必然导致结果过大。若取ξ=0,则可得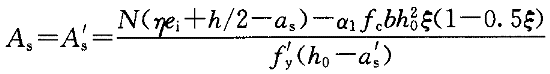

下面再采用观点(2)计算如下:
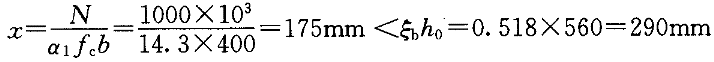
按照大偏心进行计算。于是

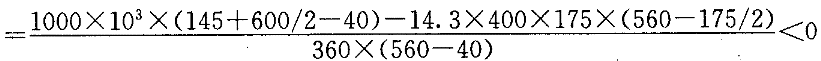
说明只需要按照构造要求配筋。
根据混凝土规范的9.5.1条,受压构件全部纵向钢筋最小配筋率为0.6%,一侧纵向钢筋最小配筋率为0.2%,由于采用HRB400钢筋,全部纵向钢筋最小配筋率减小为0.5%。于是一侧钢筋配筋率为0.25%,即A
 =A
=A =0.25%×400×600=600mm
=0.25%×400×600=600mm 。
。那么,取A
 =A
=A =600mm
=600mm ,a
,a =a
=a =40mm,是否满足承载力要求呢?
=40mm,是否满足承载力要求呢?今按照已知N求M对承载力进行复核如下。
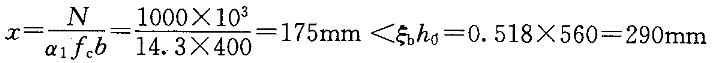
按照大偏心受压考虑。

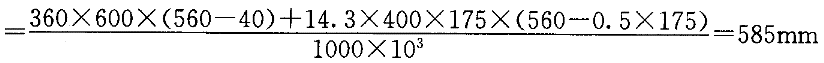
根据e与ηe
 ,的关系,可知
,的关系,可知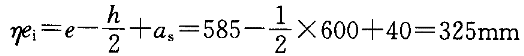
由于
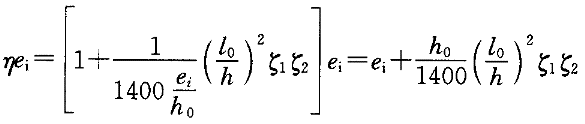
故
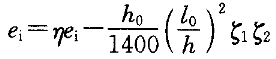
今
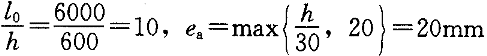 。
。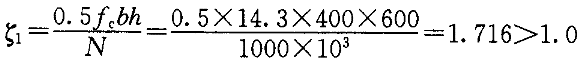 ,取ξ
,取ξ =1.0
=1.0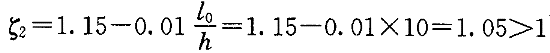 ,取ξ
,取ξ =1.0
=1.0于是可以解出:
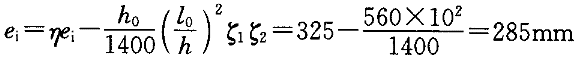
e
 =e
=e -e
-e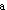 =285-20=265mm
=285-20=265mm截面h方向可承受的弯矩为
M
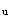 =Ne
=Ne =1000×0.265=265kN.m>85kN.m
=1000×0.265=265kN.m>85kN.m可见,承载力满足要求。
综上可见,对称配筋偏心受压构件当计算所需纵向钢筋截面积时,步骤为:
(1)计算混凝土相对受压区高度:
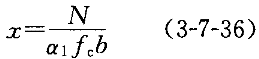
(2)若满足适用条件χ≤ξ
 h
h 且χ≥2a
且χ≥2a ,则利用下式计算配筋量:
,则利用下式计算配筋量: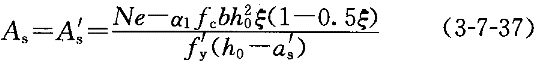
若χ≤ξ
 h
h 但χ<2a
但χ<2a ,此时受压钢筋A
,此时受压钢筋A 没有屈服。取χ=2a
没有屈服。取χ=2a ,然后对A
,然后对A 合力点取矩,得到
合力点取矩,得到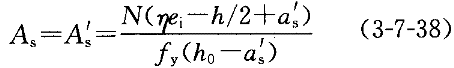
(3)若χ>ξ
 h
h ,利用下式先求出ξ,然后再计算A
,利用下式先求出ξ,然后再计算A =A
=A 。
。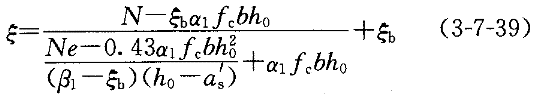
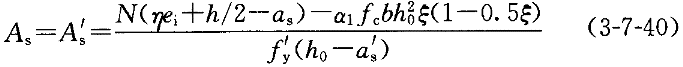
4.总结
笔者将偏心受压构件的内容归纳如下:
(1)最好不要采用"大偏心受压构件"、"小偏心受压构件"这样的称谓,因为容易产生误解,以为构件本身是"大偏心受压构件"或者"小偏心受压构件"。实际上,大、小偏心只是两种破坏形式的通俗称呼,而且并不规范。ArthurH.Nilson在其名著《DesignofConcreteStructures》-书中,将破坏类型称作"tension-controlledfailure"(受拉控制的破坏)、"compression-controlledfailure"(受压控制的破坏),笔者认为更恰当。 (2)大、小偏心破坏并不只是与偏心距有关,还与轴向力的大小以及配筋情况有关。
(3)矩形截面偏心受压柱,若采用对称配筋,在截面设计时,直接利用
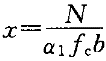 判别大小偏心。
判别大小偏心。(4)偏心受压构件的计算看起来公式很长,步骤很多,其本质,只不过是依据计算简图建立平衡方程然后解方程而已(由于《混凝土结构设计规范》GB50010-2002规定了σ
 的线性简化计算公式,因此最多只是解一元二次方程;《公路钢筋混凝土及预应力混凝土桥涵设计规范》JTGD62-2004中未规定σ
的线性简化计算公式,因此最多只是解一元二次方程;《公路钢筋混凝土及预应力混凝土桥涵设计规范》JTGD62-2004中未规定σ 的简化计算公式,会出现解一元三次方程的情况)。
的简化计算公式,会出现解一元三次方程的情况)。(5)平衡方程依据力的平衡和弯矩的平衡建立,独立方程只有两个。适用条件是为了保证平衡方程的正确性。χ≤ξ
 h
h 是为了保证A
是为了保证A f
f 的正确性;χ≥2a
的正确性;χ≥2a 是为了保证f
是为了保证f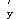 A
A 的正确性;
的正确性;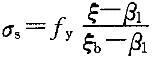 只有在-f
只有在-f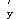 和f
和f 之间才是正确的。
之间才是正确的。 