6.连续梁的内力与调幅
正确答案:
6.塑性铰与内力重分布
(1)塑性铰的概念
受纯弯矩作用的简支钢梁,随着外弯矩的增大,在梁的某一位置处,其截面应力首先是边缘纤维达到屈服,之后塑性向内部扩展,最终截面正应力全部达到f ,对应的弯矩称作全塑性弯矩M
,对应的弯矩称作全塑性弯矩M 。此时,梁的曲率可以任意增长而弯矩维持M
。此时,梁的曲率可以任意增长而弯矩维持M ,称作形成了塑性铰。当足够多的塑性铰出现以致形成机构时,意味着承载能力的丧失(简支梁一旦出现一个塑性铰形成三铰机构即破坏)。
,称作形成了塑性铰。当足够多的塑性铰出现以致形成机构时,意味着承载能力的丧失(简支梁一旦出现一个塑性铰形成三铰机构即破坏)。
(2)内力重分布
今以图3-6-1(a)所示的两端固定梁为例说明。按照弹性状态分析时,其弯矩图如图3-6-1(b)所示,两端弯矩最大,为qι /12,依据叠加原理,跨中弯矩为qι
/12,依据叠加原理,跨中弯矩为qι /8_qι
/8_qι /12=qι
/12=qι /24。随着外荷载的增大,塑性铰首先在弯矩较大的两端出现,表现为弯矩达到塑性铰弯矩M
/24。随着外荷载的增大,塑性铰首先在弯矩较大的两端出现,表现为弯矩达到塑性铰弯矩M ,此时,外荷载仍然能够增大,直到跨中也出现塑性铰(弯矩达到Mp)形成三铰机构。依据叠加原理可知,此时应有Mp-(-Mp)=qι
,此时,外荷载仍然能够增大,直到跨中也出现塑性铰(弯矩达到Mp)形成三铰机构。依据叠加原理可知,此时应有Mp-(-Mp)=qι /8,故最终的弯矩图如图3-6-1(c)所示。此时,梁的最大弯矩为qι
/8,故最终的弯矩图如图3-6-1(c)所示。此时,梁的最大弯矩为qι /16,小于弹性分析的qι
/16,小于弹性分析的qι /12。
/12。
可见,由于塑性铰的出现,使得受力模型发生变化,从而内力发生重分布。
对于钢筋混凝土结构,内力重分布需要考虑以下几个因素:
①塑性铰的转动能力。这与纵筋配筋率、钢筋种类、混凝土的极限压应变值有关。
②斜截面承载能力。即在形成机构前,不能因斜截面承载能力不足而破坏。
③正常使用条件。为了保证裂缝不能过宽、挠度不致过大,必须对允许转动量加以控制。
考虑塑性铰引起的内力重分布,在钢结构中,是采用塑性设计;在混凝土结构中,采用调幅法。
2.连续梁的内力调幅
下面先介绍按照弹性阶段连续梁的内力计算,再介绍调幅法。
(1)连续梁的内力计算(弹性方法)
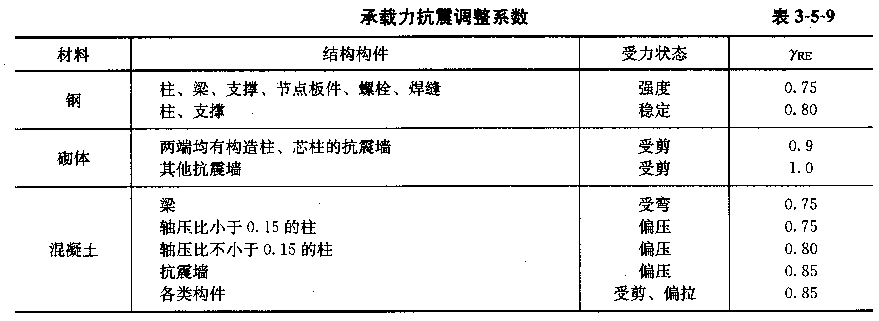
连续梁属于超静定结构,手工计算时,大多采用查表来实现。今以三跨连续梁为例,其计算表格如表3-6-1所示(通常的文献中该表格荷载情况更多,今只是为了说明问题,故从简)。
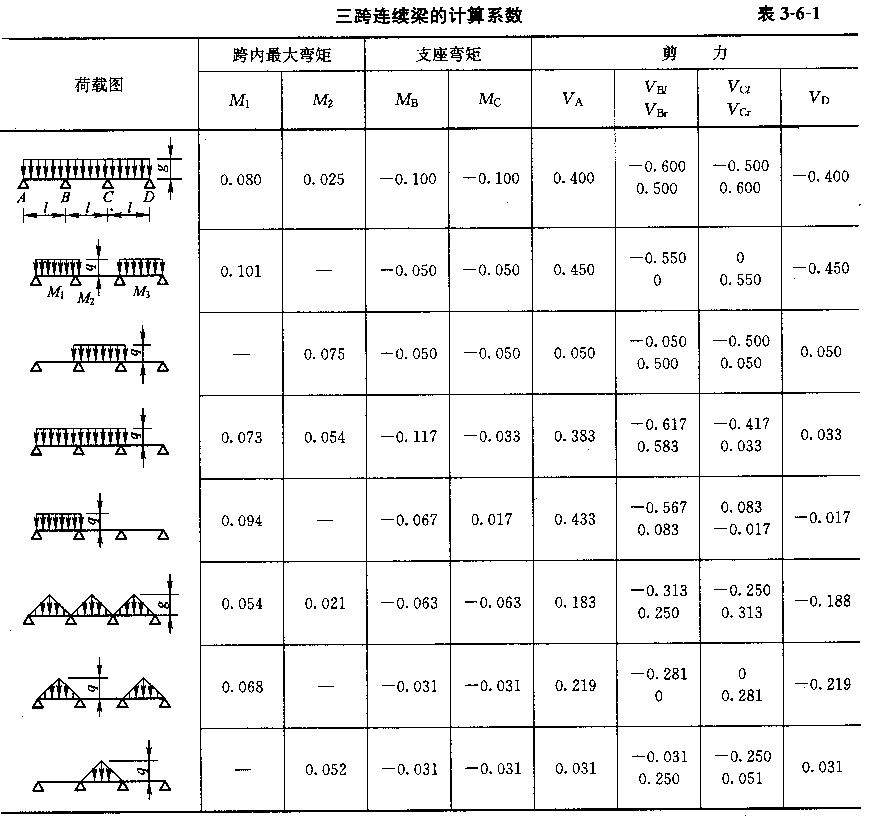
这时,在均布及三角形荷载作用下,有:
M=表中系数×qι ,V=表中系数×qι
,V=表中系数×qι
例如,三跨满布均布荷载时,边跨最大弯矩为 ,支座B处弯矩为
,支座B处弯矩为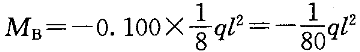 ,B支座左侧剪力值为
,B支座左侧剪力值为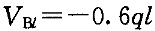 。
。
由于弹性阶段叠加原理可以适用,所以,对于需要考虑活荷载最不利布置的情况,也可方便处理。
(2)弯矩调幅
以下依据《钢筋混凝土连续梁和框架考虑内力重分布设计规程》CECS51:93(以下简称为"规程")阐述。
所谓弯矩调幅,就是对结构按照弹性理论算得的弯矩值进行适当调整。弯矩调幅系数用β表示,其定义式为
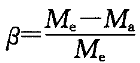
式中M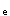 -按弹性理论算得的弯矩值;
-按弹性理论算得的弯矩值;
M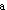 -调幅后的弯矩值。
-调幅后的弯矩值。
调幅法按照下列步骤进行:
①考虑荷载的最不利布置,按线弹性方法计算弯矩值。
②当连续梁搁置在墙上时,各支座截面弯矩值按照下式计算(4.1.6.3条):
M=(1-β)M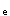
对于β的取值,"规程"规定,在弹性分析的基础上,降低连续梁(板)各支座截面的弯矩,其调幅系数不宜超过0.20(见4.1.6.2条、4.2.4.2条)。
③结构的跨中弯矩,应取按照弹性分析所得的最不利弯矩和按照下式计算所得值的较大者(4.1.6.4条):
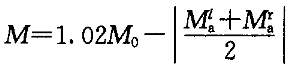
式中M -按照简支梁计算的跨中弯矩设计值;
-按照简支梁计算的跨中弯矩设计值;
M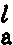 、M
、M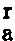 -连续梁左、右支座经调整后的弯矩设计值。
-连续梁左、右支座经调整后的弯矩设计值。
④弯矩调整后,各控制截面的弯矩值不宜小于简支弯矩值的1/3(3.0.3.3条)。
⑤各控制截面的剪力设计值按照荷载最不利布置和调幅后的支座弯矩由静力平衡条件确定。
(1)塑性铰的概念
受纯弯矩作用的简支钢梁,随着外弯矩的增大,在梁的某一位置处,其截面应力首先是边缘纤维达到屈服,之后塑性向内部扩展,最终截面正应力全部达到f
 ,对应的弯矩称作全塑性弯矩M
,对应的弯矩称作全塑性弯矩M 。此时,梁的曲率可以任意增长而弯矩维持M
。此时,梁的曲率可以任意增长而弯矩维持M ,称作形成了塑性铰。当足够多的塑性铰出现以致形成机构时,意味着承载能力的丧失(简支梁一旦出现一个塑性铰形成三铰机构即破坏)。
,称作形成了塑性铰。当足够多的塑性铰出现以致形成机构时,意味着承载能力的丧失(简支梁一旦出现一个塑性铰形成三铰机构即破坏)。(2)内力重分布
今以图3-6-1(a)所示的两端固定梁为例说明。按照弹性状态分析时,其弯矩图如图3-6-1(b)所示,两端弯矩最大,为qι
 /12,依据叠加原理,跨中弯矩为qι
/12,依据叠加原理,跨中弯矩为qι /8_qι
/8_qι /12=qι
/12=qι /24。随着外荷载的增大,塑性铰首先在弯矩较大的两端出现,表现为弯矩达到塑性铰弯矩M
/24。随着外荷载的增大,塑性铰首先在弯矩较大的两端出现,表现为弯矩达到塑性铰弯矩M ,此时,外荷载仍然能够增大,直到跨中也出现塑性铰(弯矩达到Mp)形成三铰机构。依据叠加原理可知,此时应有Mp-(-Mp)=qι
,此时,外荷载仍然能够增大,直到跨中也出现塑性铰(弯矩达到Mp)形成三铰机构。依据叠加原理可知,此时应有Mp-(-Mp)=qι /8,故最终的弯矩图如图3-6-1(c)所示。此时,梁的最大弯矩为qι
/8,故最终的弯矩图如图3-6-1(c)所示。此时,梁的最大弯矩为qι /16,小于弹性分析的qι
/16,小于弹性分析的qι /12。
/12。
可见,由于塑性铰的出现,使得受力模型发生变化,从而内力发生重分布。
对于钢筋混凝土结构,内力重分布需要考虑以下几个因素:
①塑性铰的转动能力。这与纵筋配筋率、钢筋种类、混凝土的极限压应变值有关。
②斜截面承载能力。即在形成机构前,不能因斜截面承载能力不足而破坏。
③正常使用条件。为了保证裂缝不能过宽、挠度不致过大,必须对允许转动量加以控制。
考虑塑性铰引起的内力重分布,在钢结构中,是采用塑性设计;在混凝土结构中,采用调幅法。
2.连续梁的内力调幅
下面先介绍按照弹性阶段连续梁的内力计算,再介绍调幅法。
(1)连续梁的内力计算(弹性方法)
连续梁属于超静定结构,手工计算时,大多采用查表来实现。今以三跨连续梁为例,其计算表格如表3-6-1所示(通常的文献中该表格荷载情况更多,今只是为了说明问题,故从简)。

这时,在均布及三角形荷载作用下,有:
M=表中系数×qι
 ,V=表中系数×qι
,V=表中系数×qι例如,三跨满布均布荷载时,边跨最大弯矩为
 ,支座B处弯矩为
,支座B处弯矩为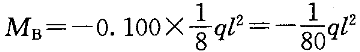 ,B支座左侧剪力值为
,B支座左侧剪力值为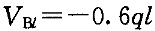 。
。由于弹性阶段叠加原理可以适用,所以,对于需要考虑活荷载最不利布置的情况,也可方便处理。
(2)弯矩调幅
以下依据《钢筋混凝土连续梁和框架考虑内力重分布设计规程》CECS51:93(以下简称为"规程")阐述。
所谓弯矩调幅,就是对结构按照弹性理论算得的弯矩值进行适当调整。弯矩调幅系数用β表示,其定义式为
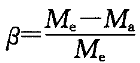
式中M
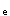 -按弹性理论算得的弯矩值;
-按弹性理论算得的弯矩值;M
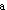 -调幅后的弯矩值。
-调幅后的弯矩值。调幅法按照下列步骤进行:
①考虑荷载的最不利布置,按线弹性方法计算弯矩值。
②当连续梁搁置在墙上时,各支座截面弯矩值按照下式计算(4.1.6.3条):
M=(1-β)M
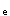
对于β的取值,"规程"规定,在弹性分析的基础上,降低连续梁(板)各支座截面的弯矩,其调幅系数不宜超过0.20(见4.1.6.2条、4.2.4.2条)。
③结构的跨中弯矩,应取按照弹性分析所得的最不利弯矩和按照下式计算所得值的较大者(4.1.6.4条):
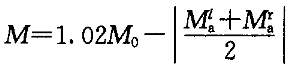
式中M
 -按照简支梁计算的跨中弯矩设计值;
-按照简支梁计算的跨中弯矩设计值;M
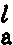 、M
、M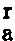 -连续梁左、右支座经调整后的弯矩设计值。
-连续梁左、右支座经调整后的弯矩设计值。④弯矩调整后,各控制截面的弯矩值不宜小于简支弯矩值的1/3(3.0.3.3条)。
⑤各控制截面的剪力设计值按照荷载最不利布置和调幅后的支座弯矩由静力平衡条件确定。
