3.分层法、反弯点法与D值法
正确答案:
3.分层法、反弯点法和D值法被用来对多层框架结构的内力进行近似计算。分层法处理的是竖向荷载作用的情况;反弯点法处理的是水平荷载作用的情况;D值法是对反弯点法的改进。
在介绍以上方法之前,先来看一些基础知识。
1.预备知识
(1)正负号的规定
在对单个构件进行应力分析或者对单个构件进行设计时,实际上是应用材料力学的知识,此时,正负号的规定通常为:轴力以拉为正压为负,弯矩以使构件截面下缘纤维受拉为正,剪力以使整个构件顺时针转动为正。
当对构件组成的结构体系进行内力分析时,手算常采用力法,电算常采用位移法。当采用位移法时,其正负号的规定为:弯矩以对杆端而言顺时针方向为正;剪力以使整个杆件顺时针转动为正;位移以使整个杆件顺时针转动为正;转角以顺时针方向为正。
(2)杆端弯矩和剪力
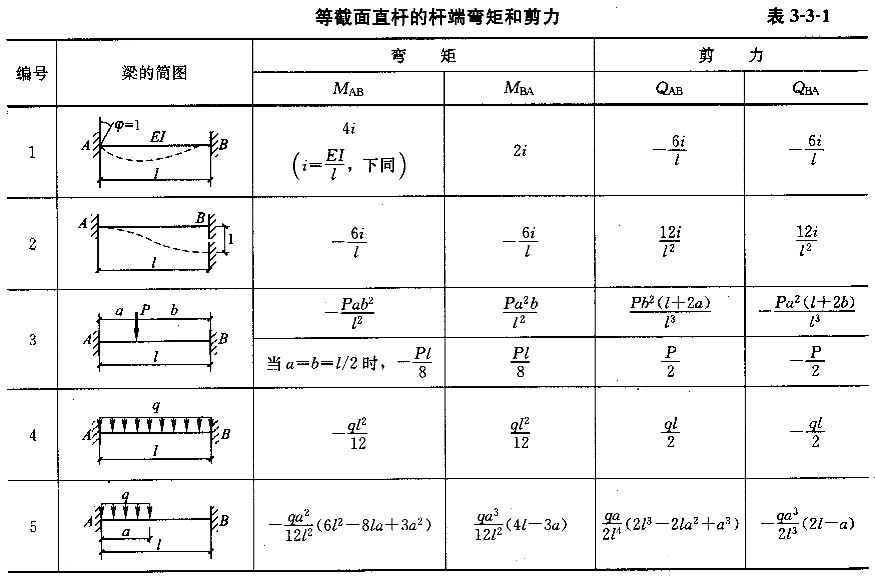
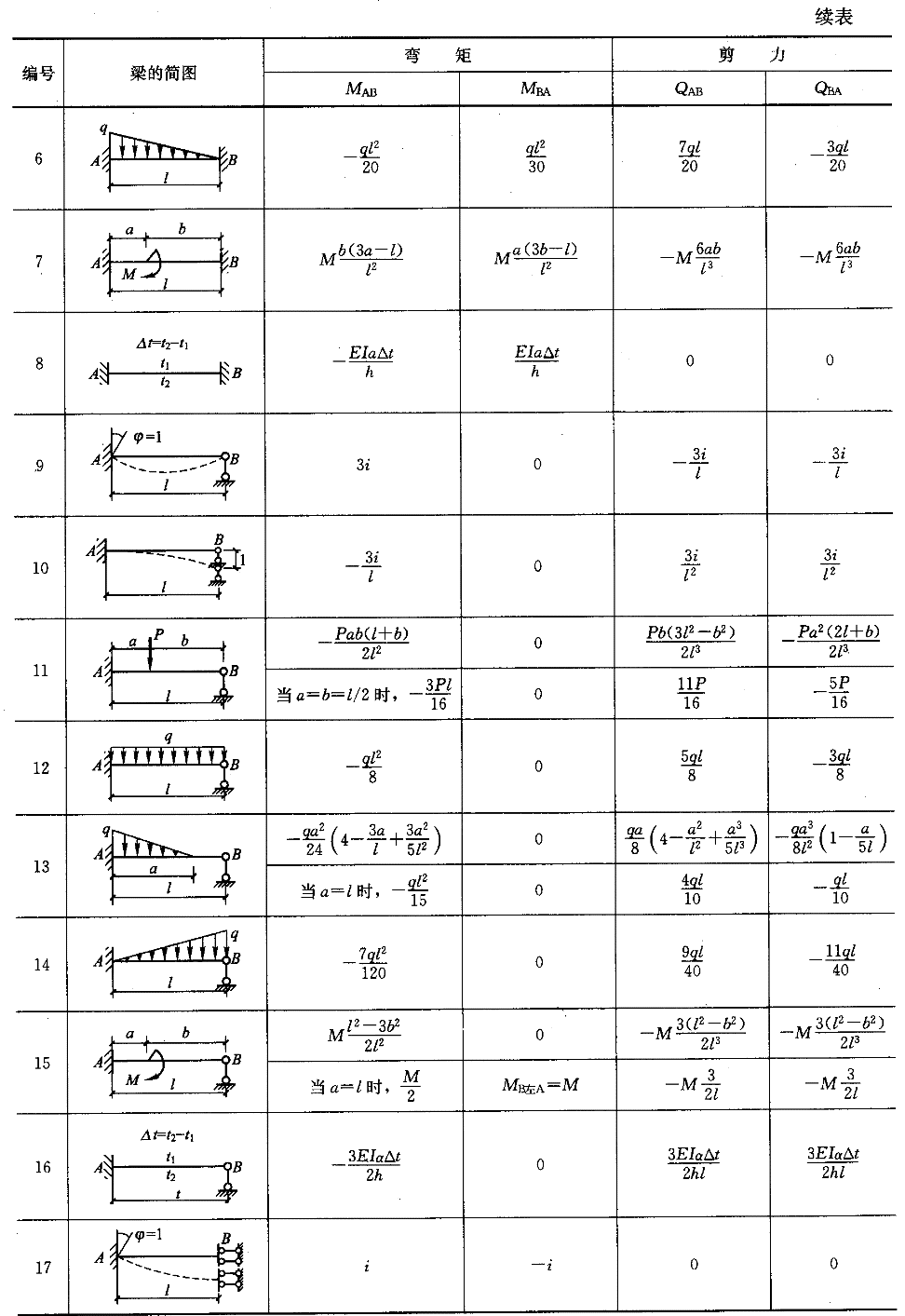
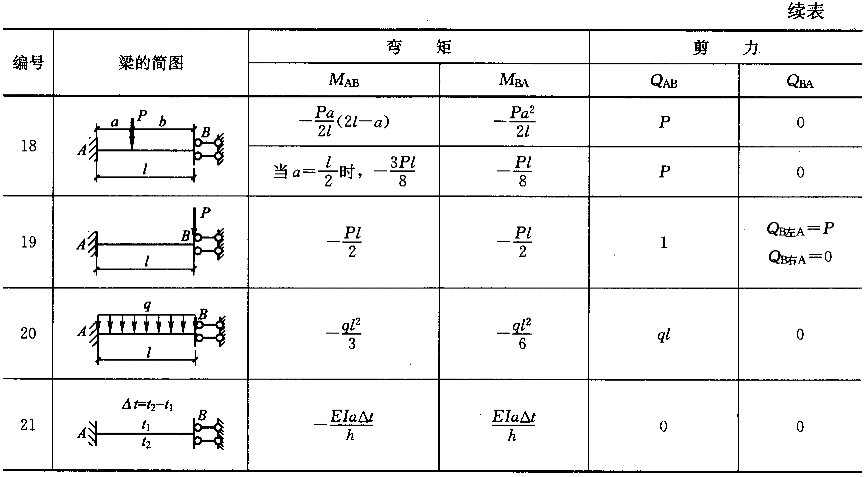
利用位移法计算时,常常用到杆端弯矩和杆端剪力,为方便使用,今将等截面单跨超静定梁在各种不同情况下的杆端弯矩和剪力列于表3-3-1。
(3)劲度系数(转动刚度)、传递系数
当杆件AB的A端转动单位角度时,A端(又称作近端)的弯矩MAB称为该杆端的劲度系数,它标志着该杆抵抗转动能力的大小,故又称转动刚度。例如,对于表3-3-1中的项次1两端固定构件,M =4i
=4i ;项次9近端固定远端铰支构件,M
;项次9近端固定远端铰支构件,M =3i
=3i ;项次17近端固定远端滑动支座构件,M
;项次17近端固定远端滑动支座构件,M =i
=i 。
。
转动刚度值不仅与杆件的线刚度i=EI/ι有关,还与杆件另一端(又称远端)的支承情况有关。当A端转动时,B端也产生一定的弯矩,就好比近端的弯矩按照一定的比例"传到"了远端,故将B端弯矩与A端弯矩之比称为A端向B端的传递系数,用C 表示,即
表示,即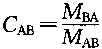 或M
或M =C
=C M
M 。由表3-3-1可知,远端为固定端时,C
。由表3-3-1可知,远端为固定端时,C =1/2;远端为铰支座时,C
=1/2;远端为铰支座时,C =0;远端为滑动支座时,C
=0;远端为滑动支座时,C =-1。
=-1。
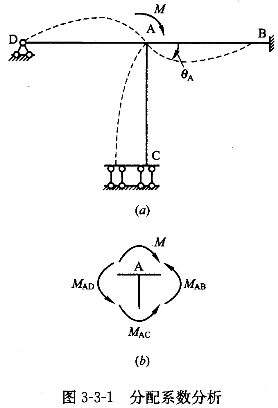
(4)分配系数
对于多个杆件交于一点的情况,如图3-3-1所示,当外力施加于节点A而使节点A产生转角,达到平衡时,由转动刚度定义可知
M =S
=S θ
θ =4i
=4i θ
θ
M =S
=S θ
θ =i
=i θ
θ
M =SADOA=i
=SADOA=i θ
θ 而在节点A处弯矩是平衡的,故
而在节点A处弯矩是平衡的,故
M +M
+M +M
+M =M
=M
从而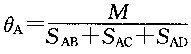
于是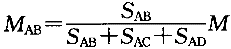
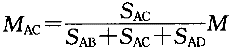
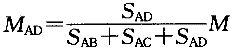
可见,各杆A端的弯矩与各杆A端的转动刚度成正比,即弯矩在A点按照各杆的转动刚度分配。令

μA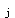 称作分配系数。显然,同一节点上各杆分配系数之和等于1.0。
称作分配系数。显然,同一节点上各杆分配系数之和等于1.0。
(5)力矩分配法
力矩分配法可采用以下步骤实现:
①固定节点:在节点处加附加约束,根据荷载求各杆端固端力矩和节点的不平衡力矩。
②放松节点:相当于在该节点处加一个与不平衡力矩反号的节点转动力矩,并使节点产生转动。
③分配:节点转动力矩按照分配系数进行分配,求出各杆近端力矩。
④传递:各杆按传递系数由近端向远端传递。
⑤叠加:各杆端的分配力矩、传递来的力矩以及固端力矩的叠加,构成杆端最后力矩。
(6)无剪力分配法
对于图3-3-2(a)的情况,将其视为图3-3-2(b)和图3-3-2(c)的叠加,即荷载分为正对称和反对称。图3-3-2(b)时节点只有转角没有侧移,故可用力矩分配法计算,而图3-3-2(c)可用无剪力分配法计算。
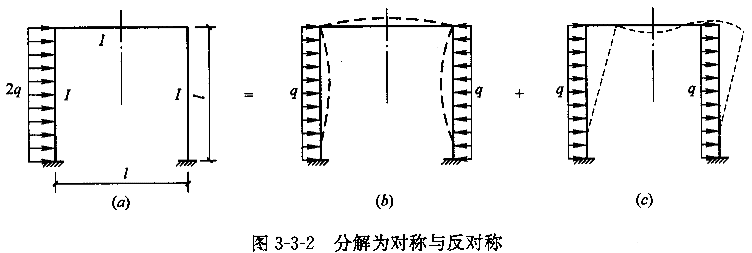
取反对称荷载作用时的半刚架如图3-3-3所示,C处为一竖向链杆支座。此半刚架的变形和受力有如下特点:横梁BC虽有水平位移但两端并无相对线位移,这称为无侧移杆件;竖杆AB两端虽有相对侧移,但由于支座C处无水平反力,故AB柱的剪力是静定的,这称作剪力静定杆件。计算此半刚架的步骤如下:
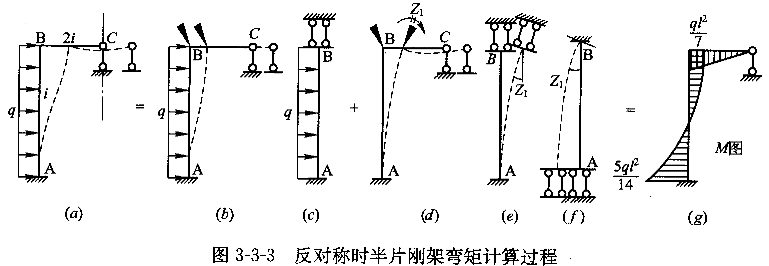
①固定节点。在节点B加一刚臂阻止转动,不阻止其线位移,如图3-3-3(b),这样,柱AB相当于下端固定上端有滑动支座。查本书表3-3-1,得到柱AB的固端弯矩为
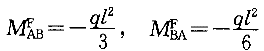
节点B的不平衡力暂时由刚臂承受。注意到B点的滑动支座不能承受水平剪力,故柱AB的两端剪力为
Q =qι,Q
=qι,Q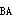 =0
=0
即全部水平荷载由柱下端的剪力所平衡。
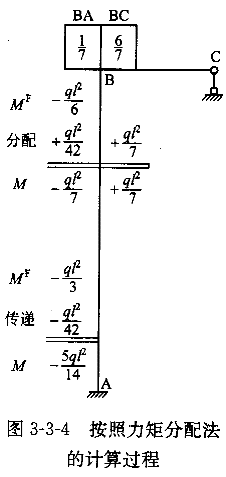
②放松节点。放松节点后,节点B不仅有转动,同时也有水平位移,如图3-3-3(d)所示。由于柱AB为下端固定上端滑动,当上端转动时柱的剪力为零,因而处于纯弯曲受力状态,这实际上与上端固定下端滑动而上端转动同样角度时的受力和变形状态完全相同,故可推知其劲度系数为1,而传递系数为-1。于是节点B的分配系数为
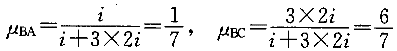
其余计算见图3-3-4,最终的弯矩图(M图)见图3-3-3(g)。
由于在力矩的分配和传递过程中,杆件的剪力为零,故称无剪力分配法。
无剪力分配法的条件是:刚架中除两端无相对线位移的杆件外,其余杆件均是剪力静定杆件。
2.分层法
分层法采用两个假定:
(1)框架在竖向荷载下侧向位移很小,可以忽略其影响;
(2)每层梁上的竖向作用对其他各层杆件内力影响不大。
因为(1),所以可使用力矩分配法;因为(2),可将框架分为多个单层框架分别计算。如图3-3-5所示的三层框架,可以分为三个单层框架分别计算,每一柱(底层柱除外)属于上下两层,柱最终的弯矩为上下层计算结果的叠加。
因为在分层计算时,假定上下柱的远端为固定端(例如图3-3-5中的E、M点),而实际上是弹性支承,为了反映这一差别,除底层外,其他层各柱的线刚度乘以0.9予以折减,传递系数也由1/2修正为1/3。
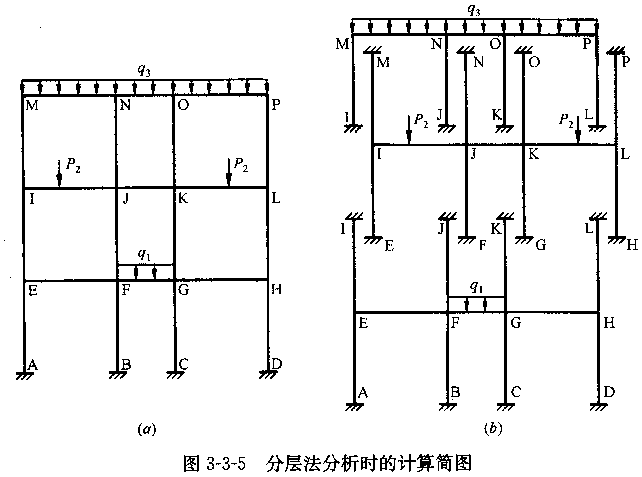
分层法最后所得结果,在刚节点上可能会存在弯矩不平衡,但误差不会很大。如有需要,可对节点不平衡弯矩再分配一次,但不平衡弯矩不再向另一端传递。
【算例】如图3-3-6所示的两跨两层框架,各杆边括号内的数字表示相对线刚度。
要求:用分层法作框架的弯矩图。
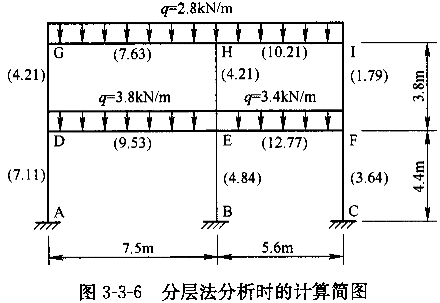
解:计算过程见图3-3-7。需要注意以下几点:
(1)对上层各柱,应将柱的线刚度乘以0.9,然后计算节点处各杆的分配系数。
例如,对于GD杆,0.9×4.21=3.79,分配系数为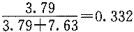 ,其他各杆分配系数写在图中的长方框内。
,其他各杆分配系数写在图中的长方框内。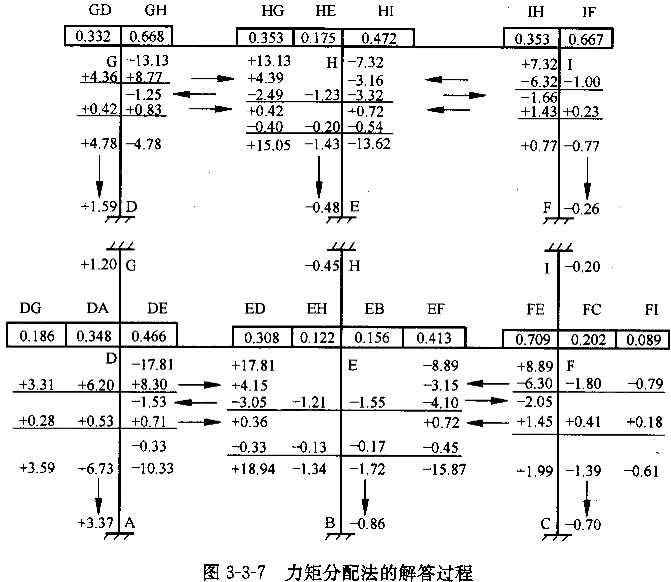
(2)查本书表3-3-1,固端弯矩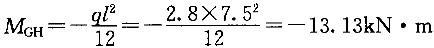 ,其他节
,其他节
点弯矩可用类似方法求得。
(3)水平向弯矩传递系数为0.5,第2层柱的弯矩传递系数为1/3,底层柱的弯矩传递系数为0.5。
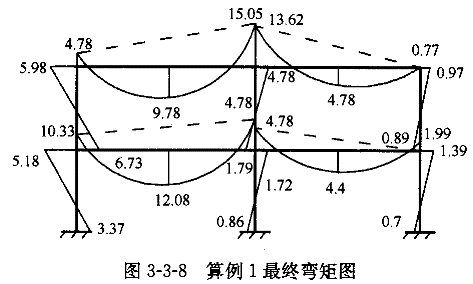
最终形成的弯矩图如图3-3-8所示。
3.反弯点法
框架所受的水平力主要是地震力和风力,它们都可以化为框架节点上的水平集中力。这时,如果框架层数不多,梁的线刚度比柱大许多(通常要求梁、柱的线刚度比≥3),而且比较规则,可以采用反弯点法进行内力计算。
反弯点法采用下述的基本假定:
(1)横梁刚度无穷大。这样,各层总剪力按照同层各柱的侧移刚度比例分配,分配时柱两端不发生角位移;
(2)各层柱的反弯点位置,除底层位于距离柱底2h/3处,其他层位于距离柱底h/2处。
所谓刚度,就是发生单位位移所需要的外力值。据此,框架结构中柱的侧移刚度就是梁端无转角但是水平位移为1时所需要的剪力,为 ,式中,i
,式中,i 为柱的线刚度,h为柱高。
为柱的线刚度,h为柱高。
所谓反弯点,是指杆件的弯矩图中竖标为零的点,在该点,弯矩被分为正弯矩和负弯矩两部分。
反弯点法的计算步骤如下:
(1)计算各柱侧移刚度,并把该层总剪力分配到各柱。
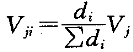
式中V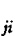 -第j层第i根柱子的剪力;
-第j层第i根柱子的剪力;
V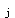 -第j层的层剪力,即第j层以上所有水平荷载总和;
-第j层的层剪力,即第j层以上所有水平荷载总和;
d -第j层第i根柱子的侧移刚度。
-第j层第i根柱子的侧移刚度。
(2)根据各柱分配到的剪力及反弯点位置,计算柱端弯矩。
底层柱:
上端弯矩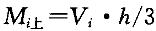
下端弯矩
其他柱:
上、下端弯矩相等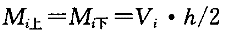
(3)根据节点平衡计算梁端弯矩,如图3-3-9所示。
对于边柱(图3-3-9a)
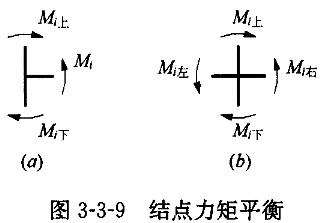
对于中柱(图3-3-9b),设梁的端弯矩与梁的线刚度成
正比,则有
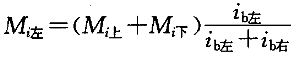
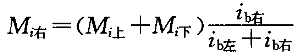
(4)由梁端弯矩,根据平衡条件,可求得梁端剪力;再根据梁端剪力,由节点平衡求
得柱的轴力。
4.D值法
D值法是对反弯点法的改进。对于层数较多的框架,由于柱轴力大,柱截面也随着增大,梁、柱线刚度比就较接近,不再符合反弯点法的假定(1);另外,反弯点的位置与柱上下端的转角大小有关(转角大小取决于约束条件),将各柱的反弯点高度统一取为定值会造成误差。
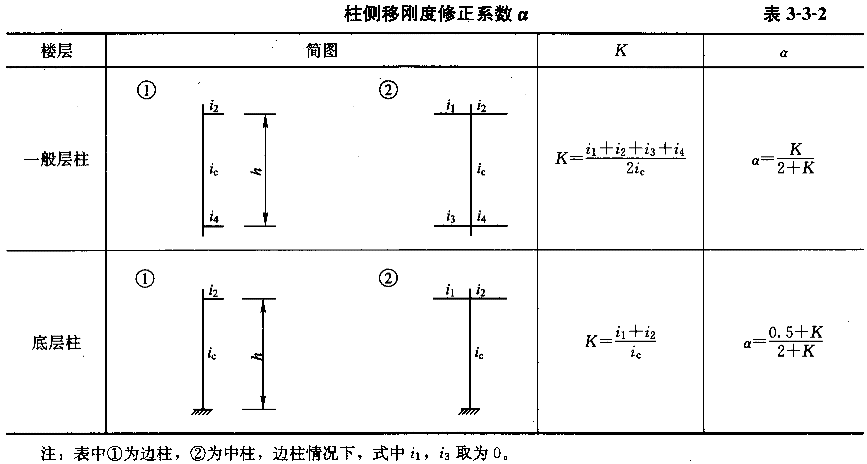
(1)柱侧移刚度的修正
D值法对柱的侧移刚度采用下式计算:
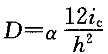
修正系数α按照表3-3-2取值。
(2)反弯点高度
反弯点到柱下端的距离与柱高的比值,称作反弯点高度比,记作y,y可按照下式求得:
y=y +y
+y +y
+y +y
+y 式中,y
式中,y 为标准反弯点高度比,是在各层等高、各跨相等、各层梁柱与线刚度不变的情况下的反弯点高度比;y
为标准反弯点高度比,是在各层等高、各跨相等、各层梁柱与线刚度不变的情况下的反弯点高度比;y 为考虑到柱上、下端相连的梁刚度不等时的反弯点高度比修正值,对于底层,不考虑y
为考虑到柱上、下端相连的梁刚度不等时的反弯点高度比修正值,对于底层,不考虑y 。将上层层高与本层层高之比h
。将上层层高与本层层高之比h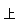 /h=α
/h=α ,由α
,由α 查表得到y
查表得到y 。同理,令下层层高与本层层高之比h
。同理,令下层层高与本层层高之比h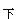 /h=a3,由α
/h=a3,由α 查表得到y
查表得到y 。最上层不考虑y
。最上层不考虑y 修正,最下层不考虑y
修正,最下层不考虑y 修正。
修正。
文献中通常都给出了以上y 、y
、y 、y
、y 、y
、y 的表格,为节省篇幅,这里从略。
的表格,为节省篇幅,这里从略。
在确定了D值(侧移刚度)与反弯点高度之后,即可按照与反弯点法相同的步骤进行计算。
在介绍以上方法之前,先来看一些基础知识。
1.预备知识
(1)正负号的规定
在对单个构件进行应力分析或者对单个构件进行设计时,实际上是应用材料力学的知识,此时,正负号的规定通常为:轴力以拉为正压为负,弯矩以使构件截面下缘纤维受拉为正,剪力以使整个构件顺时针转动为正。
当对构件组成的结构体系进行内力分析时,手算常采用力法,电算常采用位移法。当采用位移法时,其正负号的规定为:弯矩以对杆端而言顺时针方向为正;剪力以使整个杆件顺时针转动为正;位移以使整个杆件顺时针转动为正;转角以顺时针方向为正。
(2)杆端弯矩和剪力
利用位移法计算时,常常用到杆端弯矩和杆端剪力,为方便使用,今将等截面单跨超静定梁在各种不同情况下的杆端弯矩和剪力列于表3-3-1。



(3)劲度系数(转动刚度)、传递系数
当杆件AB的A端转动单位角度时,A端(又称作近端)的弯矩MAB称为该杆端的劲度系数,它标志着该杆抵抗转动能力的大小,故又称转动刚度。例如,对于表3-3-1中的项次1两端固定构件,M
 =4i
=4i ;项次9近端固定远端铰支构件,M
;项次9近端固定远端铰支构件,M =3i
=3i ;项次17近端固定远端滑动支座构件,M
;项次17近端固定远端滑动支座构件,M =i
=i 。
。转动刚度值不仅与杆件的线刚度i=EI/ι有关,还与杆件另一端(又称远端)的支承情况有关。当A端转动时,B端也产生一定的弯矩,就好比近端的弯矩按照一定的比例"传到"了远端,故将B端弯矩与A端弯矩之比称为A端向B端的传递系数,用C
 表示,即
表示,即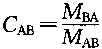 或M
或M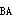 =C
=C M
M 。由表3-3-1可知,远端为固定端时,C
。由表3-3-1可知,远端为固定端时,C =1/2;远端为铰支座时,C
=1/2;远端为铰支座时,C =0;远端为滑动支座时,C
=0;远端为滑动支座时,C =-1。
=-1。
(4)分配系数
对于多个杆件交于一点的情况,如图3-3-1所示,当外力施加于节点A而使节点A产生转角,达到平衡时,由转动刚度定义可知
M
 =S
=S θ
θ =4i
=4i θ
θ
M
 =S
=S θ
θ =i
=i θ
θ
M
 =SADOA=i
=SADOA=i θ
θ 而在节点A处弯矩是平衡的,故
而在节点A处弯矩是平衡的,故M
 +M
+M +M
+M =M
=M从而
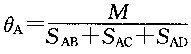
于是
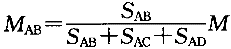

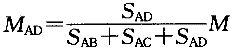
可见,各杆A端的弯矩与各杆A端的转动刚度成正比,即弯矩在A点按照各杆的转动刚度分配。令

μA
 称作分配系数。显然,同一节点上各杆分配系数之和等于1.0。
称作分配系数。显然,同一节点上各杆分配系数之和等于1.0。(5)力矩分配法
力矩分配法可采用以下步骤实现:
①固定节点:在节点处加附加约束,根据荷载求各杆端固端力矩和节点的不平衡力矩。
②放松节点:相当于在该节点处加一个与不平衡力矩反号的节点转动力矩,并使节点产生转动。
③分配:节点转动力矩按照分配系数进行分配,求出各杆近端力矩。
④传递:各杆按传递系数由近端向远端传递。
⑤叠加:各杆端的分配力矩、传递来的力矩以及固端力矩的叠加,构成杆端最后力矩。
(6)无剪力分配法
对于图3-3-2(a)的情况,将其视为图3-3-2(b)和图3-3-2(c)的叠加,即荷载分为正对称和反对称。图3-3-2(b)时节点只有转角没有侧移,故可用力矩分配法计算,而图3-3-2(c)可用无剪力分配法计算。

取反对称荷载作用时的半刚架如图3-3-3所示,C处为一竖向链杆支座。此半刚架的变形和受力有如下特点:横梁BC虽有水平位移但两端并无相对线位移,这称为无侧移杆件;竖杆AB两端虽有相对侧移,但由于支座C处无水平反力,故AB柱的剪力是静定的,这称作剪力静定杆件。计算此半刚架的步骤如下:

①固定节点。在节点B加一刚臂阻止转动,不阻止其线位移,如图3-3-3(b),这样,柱AB相当于下端固定上端有滑动支座。查本书表3-3-1,得到柱AB的固端弯矩为
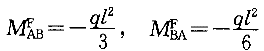
节点B的不平衡力暂时由刚臂承受。注意到B点的滑动支座不能承受水平剪力,故柱AB的两端剪力为
Q
 =qι,Q
=qι,Q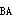 =0
=0即全部水平荷载由柱下端的剪力所平衡。
②放松节点。放松节点后,节点B不仅有转动,同时也有水平位移,如图3-3-3(d)所示。由于柱AB为下端固定上端滑动,当上端转动时柱的剪力为零,因而处于纯弯曲受力状态,这实际上与上端固定下端滑动而上端转动同样角度时的受力和变形状态完全相同,故可推知其劲度系数为1,而传递系数为-1。于是节点B的分配系数为
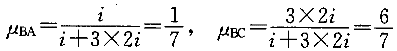
其余计算见图3-3-4,最终的弯矩图(M图)见图3-3-3(g)。
由于在力矩的分配和传递过程中,杆件的剪力为零,故称无剪力分配法。

无剪力分配法的条件是:刚架中除两端无相对线位移的杆件外,其余杆件均是剪力静定杆件。
2.分层法
分层法采用两个假定:
(1)框架在竖向荷载下侧向位移很小,可以忽略其影响;
(2)每层梁上的竖向作用对其他各层杆件内力影响不大。
因为(1),所以可使用力矩分配法;因为(2),可将框架分为多个单层框架分别计算。如图3-3-5所示的三层框架,可以分为三个单层框架分别计算,每一柱(底层柱除外)属于上下两层,柱最终的弯矩为上下层计算结果的叠加。
因为在分层计算时,假定上下柱的远端为固定端(例如图3-3-5中的E、M点),而实际上是弹性支承,为了反映这一差别,除底层外,其他层各柱的线刚度乘以0.9予以折减,传递系数也由1/2修正为1/3。

分层法最后所得结果,在刚节点上可能会存在弯矩不平衡,但误差不会很大。如有需要,可对节点不平衡弯矩再分配一次,但不平衡弯矩不再向另一端传递。
【算例】如图3-3-6所示的两跨两层框架,各杆边括号内的数字表示相对线刚度。
要求:用分层法作框架的弯矩图。

解:计算过程见图3-3-7。需要注意以下几点:
(1)对上层各柱,应将柱的线刚度乘以0.9,然后计算节点处各杆的分配系数。
例如,对于GD杆,0.9×4.21=3.79,分配系数为
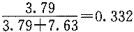 ,其他各杆分配系数写在图中的长方框内。
,其他各杆分配系数写在图中的长方框内。
(2)查本书表3-3-1,固端弯矩
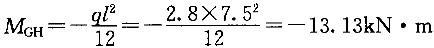 ,其他节
,其他节点弯矩可用类似方法求得。
(3)水平向弯矩传递系数为0.5,第2层柱的弯矩传递系数为1/3,底层柱的弯矩传递系数为0.5。
最终形成的弯矩图如图3-3-8所示。

3.反弯点法
框架所受的水平力主要是地震力和风力,它们都可以化为框架节点上的水平集中力。这时,如果框架层数不多,梁的线刚度比柱大许多(通常要求梁、柱的线刚度比≥3),而且比较规则,可以采用反弯点法进行内力计算。
反弯点法采用下述的基本假定:
(1)横梁刚度无穷大。这样,各层总剪力按照同层各柱的侧移刚度比例分配,分配时柱两端不发生角位移;
(2)各层柱的反弯点位置,除底层位于距离柱底2h/3处,其他层位于距离柱底h/2处。
所谓刚度,就是发生单位位移所需要的外力值。据此,框架结构中柱的侧移刚度就是梁端无转角但是水平位移为1时所需要的剪力,为
 ,式中,i
,式中,i 为柱的线刚度,h为柱高。
为柱的线刚度,h为柱高。所谓反弯点,是指杆件的弯矩图中竖标为零的点,在该点,弯矩被分为正弯矩和负弯矩两部分。
反弯点法的计算步骤如下:
(1)计算各柱侧移刚度,并把该层总剪力分配到各柱。
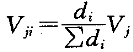
式中V
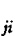 -第j层第i根柱子的剪力;
-第j层第i根柱子的剪力;V
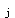 -第j层的层剪力,即第j层以上所有水平荷载总和;
-第j层的层剪力,即第j层以上所有水平荷载总和;d
 -第j层第i根柱子的侧移刚度。
-第j层第i根柱子的侧移刚度。(2)根据各柱分配到的剪力及反弯点位置,计算柱端弯矩。
底层柱:
上端弯矩
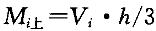
下端弯矩

其他柱:
上、下端弯矩相等
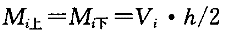
(3)根据节点平衡计算梁端弯矩,如图3-3-9所示。
对于边柱(图3-3-9a)

对于中柱(图3-3-9b),设梁的端弯矩与梁的线刚度成
正比,则有
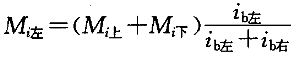
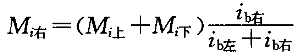
(4)由梁端弯矩,根据平衡条件,可求得梁端剪力;再根据梁端剪力,由节点平衡求
得柱的轴力。
4.D值法
D值法是对反弯点法的改进。对于层数较多的框架,由于柱轴力大,柱截面也随着增大,梁、柱线刚度比就较接近,不再符合反弯点法的假定(1);另外,反弯点的位置与柱上下端的转角大小有关(转角大小取决于约束条件),将各柱的反弯点高度统一取为定值会造成误差。
(1)柱侧移刚度的修正
D值法对柱的侧移刚度采用下式计算:
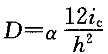
修正系数α按照表3-3-2取值。

(2)反弯点高度
反弯点到柱下端的距离与柱高的比值,称作反弯点高度比,记作y,y可按照下式求得:
y=y
 +y
+y +y
+y +y
+y 式中,y
式中,y 为标准反弯点高度比,是在各层等高、各跨相等、各层梁柱与线刚度不变的情况下的反弯点高度比;y
为标准反弯点高度比,是在各层等高、各跨相等、各层梁柱与线刚度不变的情况下的反弯点高度比;y 为考虑到柱上、下端相连的梁刚度不等时的反弯点高度比修正值,对于底层,不考虑y
为考虑到柱上、下端相连的梁刚度不等时的反弯点高度比修正值,对于底层,不考虑y 。将上层层高与本层层高之比h
。将上层层高与本层层高之比h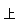 /h=α
/h=α ,由α
,由α 查表得到y
查表得到y 。同理,令下层层高与本层层高之比h
。同理,令下层层高与本层层高之比h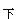 /h=a3,由α
/h=a3,由α 查表得到y
查表得到y 。最上层不考虑y
。最上层不考虑y 修正,最下层不考虑y
修正,最下层不考虑y 修正。
修正。文献中通常都给出了以上y
 、y
、y 、y
、y 、y
、y 的表格,为节省篇幅,这里从略。
的表格,为节省篇幅,这里从略。在确定了D值(侧移刚度)与反弯点高度之后,即可按照与反弯点法相同的步骤进行计算。
