2.影响线
正确答案:
2.影响线的概念
当一个指向不变的单位集中荷载(通常是竖直向下的)沿结构移动时,表示某一量值变化规律的图形,称为该量值的影响线。
例如,如图3-2-1所示的简支梁,当荷载F =1分别移动到A、1、2、3、B各等分点时,反力
=1分别移动到A、1、2、3、B各等分点时,反力 的数值分别为1、
的数值分别为1、 、
、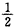 、
、 、0。如果以横坐标表示荷载F
、0。如果以横坐标表示荷载F =1的位置,以纵坐标表示F
=1的位置,以纵坐标表示F 的数值,则可将以上数值在水平的基线上用竖标绘出,再把它们的顶点相连,这就形成了F
的数值,则可将以上数值在水平的基线上用竖标绘出,再把它们的顶点相连,这就形成了F 的影响线。
的影响线。
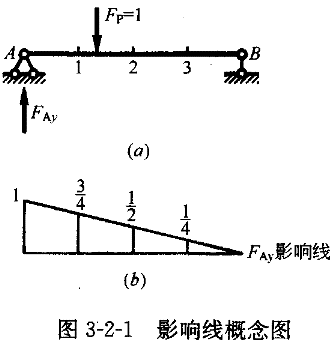
应注意区分影响线与内力图:影响线表示的是单位力在结构上移动所导致的某一个截面的内力,而内力图表示的是在荷载的作用下结构上所有截面位置的内力。
2.静定梁的影响线绘制
可以有两种方法:静力法和机动法。
(1)静力法
用静力法绘制影响线,就是依据影响线的定义,将集中单位荷载F =1作用于任意位置,并选定一坐标系,以横坐标z表示荷载作用点位置,然后依据平衡条件求出所求量值与z的函数关系,这种关系式称作"影响线方程",再根据方程作图。
=1作用于任意位置,并选定一坐标系,以横坐标z表示荷载作用点位置,然后依据平衡条件求出所求量值与z的函数关系,这种关系式称作"影响线方程",再根据方程作图。
【算例1】用静力法绘制简支梁截面C的弯矩影响线和剪力影响线。
解:如图3-2-2所示,令单位荷载F =1与A点的距离为χ,弯矩以截面下缘受拉为正,则截面C的弯矩可按下式求得:
=1与A点的距离为χ,弯矩以截面下缘受拉为正,则截面C的弯矩可按下式求得:
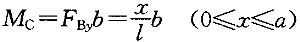

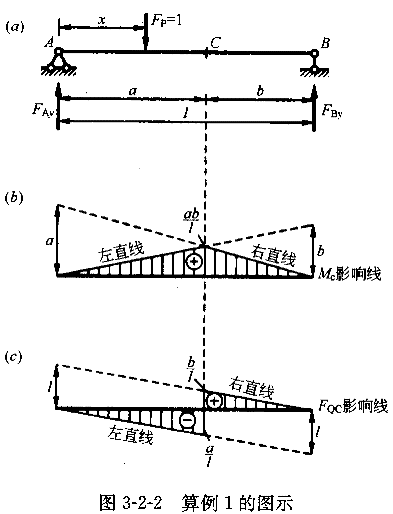
可见,M的影响线在C点以左和以右均为直线形式,在C点处为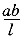 。
。
剪力以绕隔离体顺时针旋转为正,截面C的剪力可按下式求得:
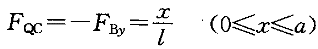

于是,F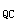 的影响线在C点以左和以右均为直线形式,在C点处会发生突变:从左侧逼近C点时,为
的影响线在C点以左和以右均为直线形式,在C点处会发生突变:从左侧逼近C点时,为 ;从右侧逼近C点时,
;从右侧逼近C点时, 。
。
(2)机动法
用机动法绘制影响线的依据是理论力学中的虚位移原理,即刚体体系在力系作用下处于平衡的充要条件是:在任何微小的虚位移中,力系所作的虚功总和为零。如图3-2-3简支梁,欲求支反力F 的影响线,首先去掉A支座处的链杆,代之以正向的反力F
的影响线,首先去掉A支座处的链杆,代之以正向的反力F ,此时原结构变成具有一个自由度的几何可变体系。然后施以微小虚位移,F
,此时原结构变成具有一个自由度的几何可变体系。然后施以微小虚位移,F 和δ
和δ 作用点沿力作用方向的虚位移分别为δ
作用点沿力作用方向的虚位移分别为δ 、δ
、δ ,则虚功方程为:
,则虚功方程为:
Xδ +F
+F δ
δ =0
=0
因F =1,故
=1,故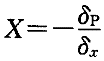
令δ =1,则上式变为X=-δ
=1,则上式变为X=-δ ,可见,δ
,可见,δ 图就代表X的影响线,只是符号相反。也就是说,F
图就代表X的影响线,只是符号相反。也就是说,F 在数值上等于δ
在数值上等于δ 。由于δ
。由于δ 以与F
以与F 方向一致为正,即以向下为正,于是可知,X的影响线以向上为正。
方向一致为正,即以向下为正,于是可知,X的影响线以向上为正。

【算例2】用机动法绘制简支梁截面C的弯矩影响线和剪力影响线。
解:如图3-2-4所示,解除与M 相应的联系,即将截面C改为铰接,并用一对力偶代替原有联系的作用,然后使AC、BC两个刚片沿Mc的正向发生虚位移,则可写出虚功方程:
相应的联系,即将截面C改为铰接,并用一对力偶代替原有联系的作用,然后使AC、BC两个刚片沿Mc的正向发生虚位移,则可写出虚功方程:
M (α+β)+F
(α+β)+F δ
δ =0故
=0故
其中,α+β是AC与BC两刚片的相对转角。若令α+β=1,则所得竖向虚位移图就表示M 的影响线。
的影响线。
解除与F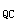 相应的联系,即将截面C改为两根水平链杆联系,使其沿F
相应的联系,即将截面C改为两根水平链杆联系,使其沿F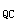 正向发生虚位移,写出虚功方程:
正向发生虚位移,写出虚功方程:
F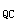 (CC
(CC +CC
+CC )+F
)+F δ
δ =0
=0
于是 若令CC
若令CC +CC
+CC =1,则所得竖向虚位移图就表示f
=1,则所得竖向虚位移图就表示f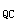 的影响线,如图3-2-4(e)所示。
的影响线,如图3-2-4(e)所示。

3.影响线的应用
(1)利用影响线求量值
若某量值的影响线已经绘出,当有若干个集中荷载作用时(如图3-2-5所示),根据叠加原理,所产生的S值为:
S=P Y
Y +P
+P y
y +…+P
+…+P y
y 式中,y
式中,y 、y
、y 、…、y
、…、y 分别对应于P
分别对应于P 、P
、P 、…、P
、…、P 作用点处的影响线竖标。
作用点处的影响线竖标。

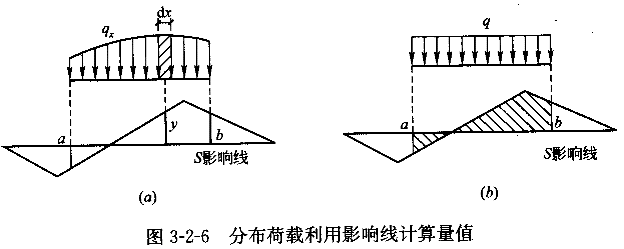
当为分布荷载时,如图3-2-6(α)所示,可将分布荷载沿长度分为无穷小的微段,则每一微段d 上的荷载q
上的荷载q d
d 可视为集中荷载,故在作用区段αb范围内的分布荷载所产生的量值S为:
可视为集中荷载,故在作用区段αb范围内的分布荷载所产生的量值S为:
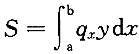
若为均布荷载,如图3-2-6(b)所示,则上式成为:

式中,ω为影响线在均布荷载范围内的面积。若该范围内影响线有正有负,则ω应为正负面积的代数和。
(2)简支梁的绝对最大弯矩
在对钢结构中的吊车梁进行设计时,会遇到简支梁的绝对最大弯矩计算问题。
由于移动荷载的作用位置不同,对于每个截面而言,都存在一个最大弯矩。在所有截面的最大弯矩中最大的那个,就是"绝对最大弯矩"。
对于这个问题,可以使用计算机方法很容易求出,步骤是:
①根据精度要求将梁分成微段,例如每微段长度为1cm,于是可得到节点χ 、χ
、χ 、…、χ
、…、χ 。
。
②做出节点χ 位置处截面的弯矩影响线。
位置处截面的弯矩影响线。
③以梁的左支座作为起点,将这组集中荷载从左向右移动,每移动1个微段长度,计算一次∑P y
y ,直到这组集中荷载的最后一个到达梁的右支座位置。这样,得到χ
,直到这组集中荷载的最后一个到达梁的右支座位置。这样,得到χ 截面弯矩的一个序列,求出这个序列的最大值,就是χ
截面弯矩的一个序列,求出这个序列的最大值,就是χ 截面在该移动荷载作用下的弯矩最大值。
截面在该移动荷载作用下的弯矩最大值。
④用同样方法,得到其他节点位置的最大弯矩。
⑤对所有节点位置的最大弯矩取最大者,这就是梁的绝对最大弯矩。
如果用手工方式计算,则应是下面的步骤:
①确定使梁中点截面发生最大弯矩的临界荷载P 。
。
②求该简支梁上可以布置的集中荷载的合力∑P 。
。
③使P 与∑P
与∑P 对称于梁的中点,此时,P
对称于梁的中点,此时,P 作用点截面的弯矩,为梁绝对最大弯矩。
作用点截面的弯矩,为梁绝对最大弯矩。
需要注意的是,以上只是正向行驶的情况。若考虑到荷载可能会反向行驶,则需要将这组集中荷载排列的先后顺序颠倒,用上述同样的步骤,得到荷载反向行驶时的绝对最大弯矩。最后,取正向时和反向时的较大者,作为最终的绝对最大弯矩。
《钢结构设计手册》中给出了吊车梁绝对最大弯矩的计算公式,思路即为上面所述的手工方式。
《钢结构设计手册》(中国建筑工业出版社,1989年)以及《钢结构设计手册》(上册,第三版,中国建筑工业出版社,2004年)给出的最大弯矩点(C点)的位置为:

最大弯矩为:
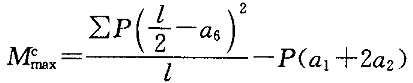
最大弯矩处的相应剪力为:
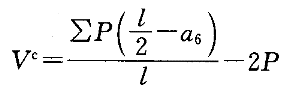
笔者研究发现,对于6个轮子作用于梁上的情况(如图3-2-7所示),《钢结构设计手册》中给出的公式值得商榷。下面以一个算例说明。

【算例3】已知吊车轮压如图3-2-8所示,P =P=611.6kN(i=1,2,…,6),ι=12m,a
=P=611.6kN(i=1,2,…,6),ι=12m,a =840mm,a
=840mm,a =3960mm,a
=3960mm,a =840mm,a
=840mm,a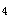 =3560mm,a
=3560mm,a =840mm,求吊车梁的绝对最大弯矩(该例题来自于1989年版《钢结构设计手册》)。
=840mm,求吊车梁的绝对最大弯矩(该例题来自于1989年版《钢结构设计手册》)。

解:P 作用于影响线顶点时,C点位置:
作用于影响线顶点时,C点位置:



反向行驶,P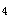 作用于影响线顶点时,C点位置:
作用于影响线顶点时,C点位置:


可见,依据《钢结构设计手册》中的公式,只能得到5133kN.m,而实际最大弯矩为5147kN.m。事实上,分析可知,只要a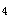 <a
<a ,手册中给出的公式就会失效。
,手册中给出的公式就会失效。
解决的办法是:把a 、a
、a 、…、a
、…、a 改为a
改为a 、a
、a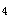 、…、a
、…、a ,仍旧代入手册公式,再计算一遍反向行驶的情况,取二者所得弯矩的较大者。
,仍旧代入手册公式,再计算一遍反向行驶的情况,取二者所得弯矩的较大者。
(3)超静定梁的最不利荷载位置
超静定梁在均布荷载作用下的最不利荷载位置,可以由影响线确定:将均布活载布置在影响线正号面积部分,得到最大值时的荷载位置,将均布活载布置在影响线负号面积部分,得到最小值时的荷载位置。因此,这里的关键问题是如何确定影响线的形状,而不是影响线的竖标值。
这时,可以应用米勒一布雷斯劳原理得到超静定梁的"定性影响线":撤除与所求内力或反力S相应的约束,使体系沿S的正向发生位移,得到的变形图即为影响线的形状。横坐标以上图形为正,横坐标以下图形为负。
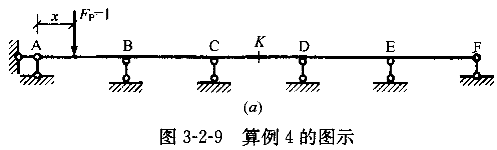
【算例4】作出图3-2-9(a)所示等截面连续梁的F 、M
、M 、M
、M 、
、 以及F
以及F 的影响线形状。
的影响线形状。
解:去掉支座C处的链杆,代之以向上的力(支座反力通常以向上为正),得到的曲线形状如图3-2-9(b)所示,即为F 的影响线。
的影响线。

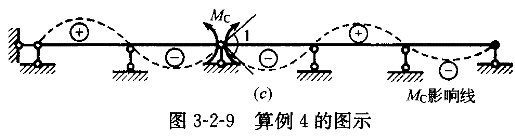
将节点C处改为铰,添加力偶(以下缘受拉为正方向),得到Mc的影响线如图3-2-9(c)所示。
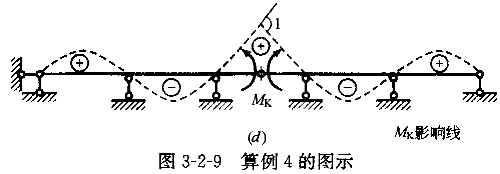
将节点K处改为铰,添加力偶(以下缘受拉为正方向),得到的曲线如图3-2-9(d)所示,此即为M 的影响线。由于K处没有支座,故曲线在CD跨不是很平滑。
的影响线。由于K处没有支座,故曲线在CD跨不是很平滑。
将支座C右侧改为两个水平链杆,就去掉了剪力的约束。剪力的正负号规定是:取隔离体,以隔离体顺时针转动为正,简称"左上右下为正"。据此施加正的剪力,得到曲线如图3-2-9(e)所示,此即为 的影响线。
的影响线。

将K处改为两个水平链杆,施加正的剪力,得到F 的影响线形状如图3-2-9(f)所示。
的影响线形状如图3-2-9(f)所示。

当一个指向不变的单位集中荷载(通常是竖直向下的)沿结构移动时,表示某一量值变化规律的图形,称为该量值的影响线。
例如,如图3-2-1所示的简支梁,当荷载F
 =1分别移动到A、1、2、3、B各等分点时,反力
=1分别移动到A、1、2、3、B各等分点时,反力 的数值分别为1、
的数值分别为1、 、
、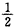 、
、 、0。如果以横坐标表示荷载F
、0。如果以横坐标表示荷载F =1的位置,以纵坐标表示F
=1的位置,以纵坐标表示F 的数值,则可将以上数值在水平的基线上用竖标绘出,再把它们的顶点相连,这就形成了F
的数值,则可将以上数值在水平的基线上用竖标绘出,再把它们的顶点相连,这就形成了F 的影响线。
的影响线。
应注意区分影响线与内力图:影响线表示的是单位力在结构上移动所导致的某一个截面的内力,而内力图表示的是在荷载的作用下结构上所有截面位置的内力。
2.静定梁的影响线绘制
可以有两种方法:静力法和机动法。
(1)静力法
用静力法绘制影响线,就是依据影响线的定义,将集中单位荷载F
 =1作用于任意位置,并选定一坐标系,以横坐标z表示荷载作用点位置,然后依据平衡条件求出所求量值与z的函数关系,这种关系式称作"影响线方程",再根据方程作图。
=1作用于任意位置,并选定一坐标系,以横坐标z表示荷载作用点位置,然后依据平衡条件求出所求量值与z的函数关系,这种关系式称作"影响线方程",再根据方程作图。【算例1】用静力法绘制简支梁截面C的弯矩影响线和剪力影响线。
解:如图3-2-2所示,令单位荷载F
 =1与A点的距离为χ,弯矩以截面下缘受拉为正,则截面C的弯矩可按下式求得:
=1与A点的距离为χ,弯矩以截面下缘受拉为正,则截面C的弯矩可按下式求得: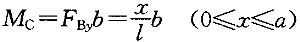


可见,M的影响线在C点以左和以右均为直线形式,在C点处为
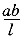 。
。剪力以绕隔离体顺时针旋转为正,截面C的剪力可按下式求得:
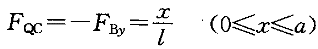

于是,F
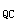 的影响线在C点以左和以右均为直线形式,在C点处会发生突变:从左侧逼近C点时,为
的影响线在C点以左和以右均为直线形式,在C点处会发生突变:从左侧逼近C点时,为 ;从右侧逼近C点时,
;从右侧逼近C点时, 。
。(2)机动法
用机动法绘制影响线的依据是理论力学中的虚位移原理,即刚体体系在力系作用下处于平衡的充要条件是:在任何微小的虚位移中,力系所作的虚功总和为零。如图3-2-3简支梁,欲求支反力F
 的影响线,首先去掉A支座处的链杆,代之以正向的反力F
的影响线,首先去掉A支座处的链杆,代之以正向的反力F ,此时原结构变成具有一个自由度的几何可变体系。然后施以微小虚位移,F
,此时原结构变成具有一个自由度的几何可变体系。然后施以微小虚位移,F 和δ
和δ 作用点沿力作用方向的虚位移分别为δ
作用点沿力作用方向的虚位移分别为δ 、δ
、δ ,则虚功方程为:
,则虚功方程为:Xδ
 +F
+F δ
δ =0
=0因F
 =1,故
=1,故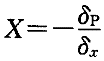
令δ
 =1,则上式变为X=-δ
=1,则上式变为X=-δ ,可见,δ
,可见,δ 图就代表X的影响线,只是符号相反。也就是说,F
图就代表X的影响线,只是符号相反。也就是说,F 在数值上等于δ
在数值上等于δ 。由于δ
。由于δ 以与F
以与F 方向一致为正,即以向下为正,于是可知,X的影响线以向上为正。
方向一致为正,即以向下为正,于是可知,X的影响线以向上为正。
【算例2】用机动法绘制简支梁截面C的弯矩影响线和剪力影响线。
解:如图3-2-4所示,解除与M
 相应的联系,即将截面C改为铰接,并用一对力偶代替原有联系的作用,然后使AC、BC两个刚片沿Mc的正向发生虚位移,则可写出虚功方程:
相应的联系,即将截面C改为铰接,并用一对力偶代替原有联系的作用,然后使AC、BC两个刚片沿Mc的正向发生虚位移,则可写出虚功方程:M
 (α+β)+F
(α+β)+F δ
δ =0故
=0故
其中,α+β是AC与BC两刚片的相对转角。若令α+β=1,则所得竖向虚位移图就表示M
 的影响线。
的影响线。解除与F
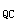 相应的联系,即将截面C改为两根水平链杆联系,使其沿F
相应的联系,即将截面C改为两根水平链杆联系,使其沿F 正向发生虚位移,写出虚功方程:
正向发生虚位移,写出虚功方程:F
 (CC
(CC +CC
+CC )+F
)+F δ
δ =0
=0于是
 若令CC
若令CC +CC
+CC =1,则所得竖向虚位移图就表示f
=1,则所得竖向虚位移图就表示f 的影响线,如图3-2-4(e)所示。
的影响线,如图3-2-4(e)所示。
3.影响线的应用
(1)利用影响线求量值
若某量值的影响线已经绘出,当有若干个集中荷载作用时(如图3-2-5所示),根据叠加原理,所产生的S值为:
S=P
 Y
Y +P
+P y
y +…+P
+…+P y
y 式中,y
式中,y 、y
、y 、…、y
、…、y 分别对应于P
分别对应于P 、P
、P 、…、P
、…、P 作用点处的影响线竖标。
作用点处的影响线竖标。
当为分布荷载时,如图3-2-6(α)所示,可将分布荷载沿长度分为无穷小的微段,则每一微段d
 上的荷载q
上的荷载q d
d 可视为集中荷载,故在作用区段αb范围内的分布荷载所产生的量值S为:
可视为集中荷载,故在作用区段αb范围内的分布荷载所产生的量值S为: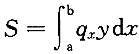
若为均布荷载,如图3-2-6(b)所示,则上式成为:

式中,ω为影响线在均布荷载范围内的面积。若该范围内影响线有正有负,则ω应为正负面积的代数和。

(2)简支梁的绝对最大弯矩
在对钢结构中的吊车梁进行设计时,会遇到简支梁的绝对最大弯矩计算问题。
由于移动荷载的作用位置不同,对于每个截面而言,都存在一个最大弯矩。在所有截面的最大弯矩中最大的那个,就是"绝对最大弯矩"。
对于这个问题,可以使用计算机方法很容易求出,步骤是:
①根据精度要求将梁分成微段,例如每微段长度为1cm,于是可得到节点χ
 、χ
、χ 、…、χ
、…、χ 。
。②做出节点χ
 位置处截面的弯矩影响线。
位置处截面的弯矩影响线。③以梁的左支座作为起点,将这组集中荷载从左向右移动,每移动1个微段长度,计算一次∑P
 y
y ,直到这组集中荷载的最后一个到达梁的右支座位置。这样,得到χ
,直到这组集中荷载的最后一个到达梁的右支座位置。这样,得到χ 截面弯矩的一个序列,求出这个序列的最大值,就是χ
截面弯矩的一个序列,求出这个序列的最大值,就是χ 截面在该移动荷载作用下的弯矩最大值。
截面在该移动荷载作用下的弯矩最大值。④用同样方法,得到其他节点位置的最大弯矩。
⑤对所有节点位置的最大弯矩取最大者,这就是梁的绝对最大弯矩。
如果用手工方式计算,则应是下面的步骤:
①确定使梁中点截面发生最大弯矩的临界荷载P
 。
。②求该简支梁上可以布置的集中荷载的合力∑P
 。
。③使P
 与∑P
与∑P 对称于梁的中点,此时,P
对称于梁的中点,此时,P 作用点截面的弯矩,为梁绝对最大弯矩。
作用点截面的弯矩,为梁绝对最大弯矩。需要注意的是,以上只是正向行驶的情况。若考虑到荷载可能会反向行驶,则需要将这组集中荷载排列的先后顺序颠倒,用上述同样的步骤,得到荷载反向行驶时的绝对最大弯矩。最后,取正向时和反向时的较大者,作为最终的绝对最大弯矩。
《钢结构设计手册》中给出了吊车梁绝对最大弯矩的计算公式,思路即为上面所述的手工方式。
《钢结构设计手册》(中国建筑工业出版社,1989年)以及《钢结构设计手册》(上册,第三版,中国建筑工业出版社,2004年)给出的最大弯矩点(C点)的位置为:

最大弯矩为:
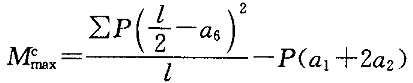
最大弯矩处的相应剪力为:
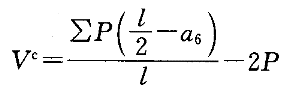
笔者研究发现,对于6个轮子作用于梁上的情况(如图3-2-7所示),《钢结构设计手册》中给出的公式值得商榷。下面以一个算例说明。

【算例3】已知吊车轮压如图3-2-8所示,P
 =P=611.6kN(i=1,2,…,6),ι=12m,a
=P=611.6kN(i=1,2,…,6),ι=12m,a =840mm,a
=840mm,a =3960mm,a
=3960mm,a =840mm,a
=840mm,a =3560mm,a
=3560mm,a =840mm,求吊车梁的绝对最大弯矩(该例题来自于1989年版《钢结构设计手册》)。
=840mm,求吊车梁的绝对最大弯矩(该例题来自于1989年版《钢结构设计手册》)。
解:P
 作用于影响线顶点时,C点位置:
作用于影响线顶点时,C点位置:


反向行驶,P
 作用于影响线顶点时,C点位置:
作用于影响线顶点时,C点位置:

可见,依据《钢结构设计手册》中的公式,只能得到5133kN.m,而实际最大弯矩为5147kN.m。事实上,分析可知,只要a
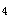 <a
<a ,手册中给出的公式就会失效。
,手册中给出的公式就会失效。解决的办法是:把a
 、a
、a 、…、a
、…、a 改为a
改为a 、a
、a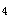 、…、a
、…、a ,仍旧代入手册公式,再计算一遍反向行驶的情况,取二者所得弯矩的较大者。
,仍旧代入手册公式,再计算一遍反向行驶的情况,取二者所得弯矩的较大者。(3)超静定梁的最不利荷载位置
超静定梁在均布荷载作用下的最不利荷载位置,可以由影响线确定:将均布活载布置在影响线正号面积部分,得到最大值时的荷载位置,将均布活载布置在影响线负号面积部分,得到最小值时的荷载位置。因此,这里的关键问题是如何确定影响线的形状,而不是影响线的竖标值。
这时,可以应用米勒一布雷斯劳原理得到超静定梁的"定性影响线":撤除与所求内力或反力S相应的约束,使体系沿S的正向发生位移,得到的变形图即为影响线的形状。横坐标以上图形为正,横坐标以下图形为负。
【算例4】作出图3-2-9(a)所示等截面连续梁的F
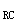 、M
、M 、M
、M 、
、 以及F
以及F 的影响线形状。
的影响线形状。
解:去掉支座C处的链杆,代之以向上的力(支座反力通常以向上为正),得到的曲线形状如图3-2-9(b)所示,即为F
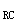 的影响线。
的影响线。
将节点C处改为铰,添加力偶(以下缘受拉为正方向),得到Mc的影响线如图3-2-9(c)所示。

将节点K处改为铰,添加力偶(以下缘受拉为正方向),得到的曲线如图3-2-9(d)所示,此即为M
 的影响线。由于K处没有支座,故曲线在CD跨不是很平滑。
的影响线。由于K处没有支座,故曲线在CD跨不是很平滑。
将支座C右侧改为两个水平链杆,就去掉了剪力的约束。剪力的正负号规定是:取隔离体,以隔离体顺时针转动为正,简称"左上右下为正"。据此施加正的剪力,得到曲线如图3-2-9(e)所示,此即为
 的影响线。
的影响线。
将K处改为两个水平链杆,施加正的剪力,得到F
 的影响线形状如图3-2-9(f)所示。
的影响线形状如图3-2-9(f)所示。
