35.如何理解等效弯矩系数β 的概念?
的概念?
 的概念?
的概念? 正确答案:
35.对于如图2-2-7(α)所示的压弯构件,当按照结构力学方法绘制弯矩图时,跨中的弯矩值称作"一阶弯矩",记作M ,显然,此时有M
,显然,此时有M =M,即与端部弯矩相等。然而,由于P-δ效应,导致跨中弯矩会"放大",成为M
=M,即与端部弯矩相等。然而,由于P-δ效应,导致跨中弯矩会"放大",成为M =M
=M +Pδ,式中的δ包括两部分,一阶挠度
+Pδ,式中的δ包括两部分,一阶挠度 (这可以由结构力学的图乘法得到),二阶挠度
(这可以由结构力学的图乘法得到),二阶挠度 ,即
,即
 ,一阶挠度被放大了
,一阶挠度被放大了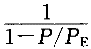 倍。P
倍。P 为欧拉临界力。
为欧拉临界力。
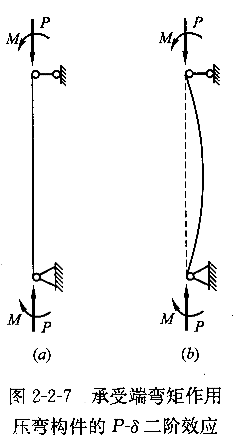
于是,对于图2-2-7(b)的情况,将有
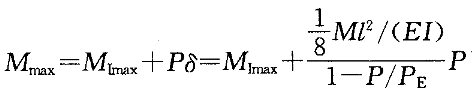
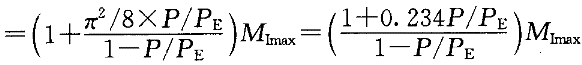
上式可以写成 式中,β
式中,β 为等效弯矩系数,A
为等效弯矩系数,A 是弯矩放大系数。
是弯矩放大系数。
对于不同的荷载情况,沿构件跨度的最大弯矩总能写成与上式类似的形式,只是β 值不同。
值不同。
等效弯矩系数的本意是:将承受轴心压力和均匀弯矩的情况作为一种基准,将其他受力情况(例如图2-2-8(α))的一阶最大弯矩乘以β ,得到M
,得到M ,按此M
,按此M 作为均匀弯矩得到的M
作为均匀弯矩得到的M 图2-2-8(b))与该受力情况按P-δ二阶算得的M
图2-2-8(b))与该受力情况按P-δ二阶算得的M 相等。这就像计算长度l
相等。这就像计算长度l ,通过乘以系数μ,其他约束情况都化成了两端简支这一基准情况。
,通过乘以系数μ,其他约束情况都化成了两端简支这一基准情况。

 ,显然,此时有M
,显然,此时有M =M,即与端部弯矩相等。然而,由于P-δ效应,导致跨中弯矩会"放大",成为M
=M,即与端部弯矩相等。然而,由于P-δ效应,导致跨中弯矩会"放大",成为M =M
=M +Pδ,式中的δ包括两部分,一阶挠度
+Pδ,式中的δ包括两部分,一阶挠度 (这可以由结构力学的图乘法得到),二阶挠度
(这可以由结构力学的图乘法得到),二阶挠度 ,即
,即 ,一阶挠度被放大了
,一阶挠度被放大了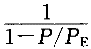 倍。P
倍。P 为欧拉临界力。
为欧拉临界力。
于是,对于图2-2-7(b)的情况,将有
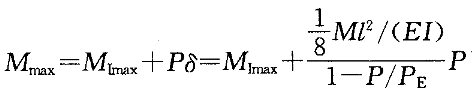
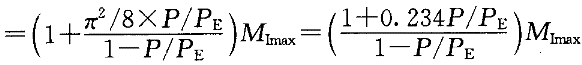
上式可以写成
 式中,β
式中,β 为等效弯矩系数,A
为等效弯矩系数,A 是弯矩放大系数。
是弯矩放大系数。对于不同的荷载情况,沿构件跨度的最大弯矩总能写成与上式类似的形式,只是β
 值不同。
值不同。等效弯矩系数的本意是:将承受轴心压力和均匀弯矩的情况作为一种基准,将其他受力情况(例如图2-2-8(α))的一阶最大弯矩乘以β
 ,得到M
,得到M ,按此M
,按此M 作为均匀弯矩得到的M
作为均匀弯矩得到的M 图2-2-8(b))与该受力情况按P-δ二阶算得的M
图2-2-8(b))与该受力情况按P-δ二阶算得的M 相等。这就像计算长度l
相等。这就像计算长度l ,通过乘以系数μ,其他约束情况都化成了两端简支这一基准情况。
,通过乘以系数μ,其他约束情况都化成了两端简支这一基准情况。
