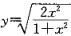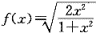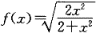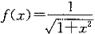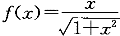曲线通过(1，1)点，且此曲线在［1，x］上所形成的曲边梯形面积的值等于该曲线终点的横坐标x与纵坐标y之比的二倍减去2，其中x>1，y>0。则当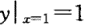
时的曲线方程为：
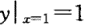时的曲线方程为： - A.
- B.
- C.
- D.
正确答案：
A
答案解析：
把方程变形，得到可分离变量的方程，求通解、特解。解法如下
y
=2(y-xy′)，y=2y-2xy′，2xy′=2y-y
[1／(2y-y)]dy=(1／2x)dx(可分离变量方程)，
)]dy=(1／2x)dx
)]dy=(1／2x)dx，
)]dy=(1／2x)dx
(1／2)lny-(1／4)(1／(2-y
)d(-y)=(1／2)lnx+c
(1／2)lny-(1／4)ln(2一y)=(1／2)lnx+c
2lny-ln(2-y)=2lnx+c
y／(2-y)=c
x
代入初始条件x=1，y=1，得1／(2-1)=c，故c=1。则
y=x(2-y)，y(1+x)=2x，y=2x／(1+x)，
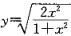
y
=2(y-xy′)，y=2y-2xy′，2xy′=2y-y[1／(2y-y
)]dy=(1／2x)dx(可分离变量方程)，)]dy=(1／2x)dx)]dy=(1／2x)dx，)]dy=(1／2x)dx(1／2)lny-(1／4)
(1／(2-y)d(-y)=(1／2)lnx+c(1／2)lny-(1／4)ln(2一y
)=(1／2)lnx+c2lny-ln(2-y
)=2lnx+cy
／(2-y)=cx代入初始条件x=1，y=1，得1／(2-1)=c
，故c=1。则y
=x(2-y)，y(1+x)=2x，y=2x／(1+x)，
