设参数方程 ,确定了y是x的函数,且f′(t)存在,f(0)=2,f′(0)=2,则当t=0时,dy/dx的值等于:
,确定了y是x的函数,且f′(t)存在,f(0)=2,f′(0)=2,则当t=0时,dy/dx的值等于:
 ,确定了y是x的函数,且f′(t)存在,f(0)=2,f′(0)=2,则当t=0时,dy/dx的值等于:
,确定了y是x的函数,且f′(t)存在,f(0)=2,f′(0)=2,则当t=0时,dy/dx的值等于: 正确答案:
D
答案解析:
利用参数方程导数公式计算出dy/dx,代入t=0,得到t=0时的dy/dx值。计算如下
dy/dt=f(t)+tf′(t)
dx/dt=f′(t)-f′(t)/f(t)
dy/dx=(dy/dt)/(dx/dt)=[f(t)+tf′(t)]/[tf′(t)-f′(x)/f(x)],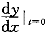 =2/(2-1)=2
=2/(2-1)=2
dy/dt=f(t)+tf′(t)
dx/dt=f′(t)-f′(t)/f(t)
dy/dx=(dy/dt)/(dx/dt)=[f(t)+tf′(t)]/[tf′(t)-f′(x)/f(x)],
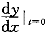 =2/(2-1)=2
=2/(2-1)=2