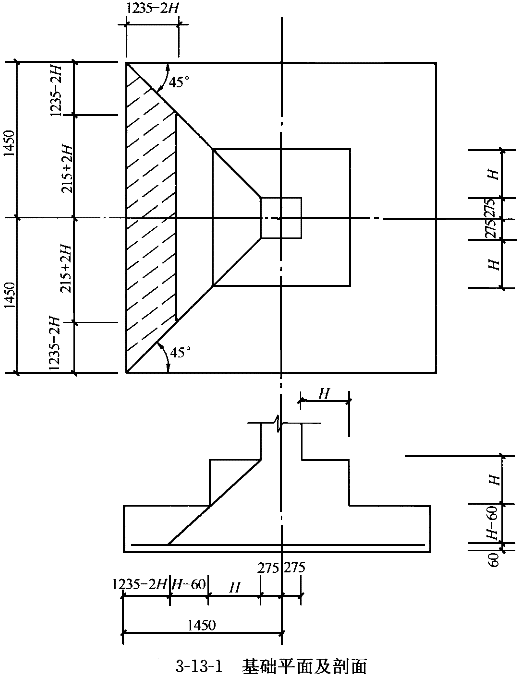
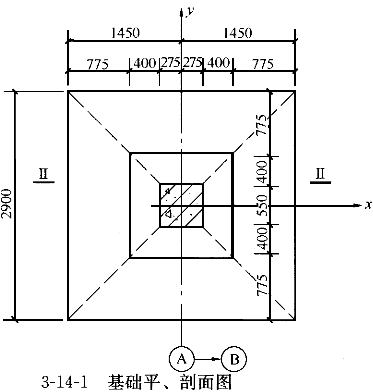
某方形截面钢筋混凝土柱,柱截面尺寸550mm×550mm,采用方形基础,其平面尺寸为2900mm×2900mm;混凝土强度等级C30,采用HRB400级钢筋;非抗震设计,γ =1.0,a
=1.0,a =60mm。见图3-13-1。
=60mm。见图3-13-1。
 =1.0,a
=1.0,a =60mm。见图3-13-1。
=60mm。见图3-13-1。
- 现已算出在轴向压力作用下,基础底面处所受的相应于荷载效应标准组合的净反力标准值为300kPa;基础受冲切承载力按《建筑地基基础设计规范》式(3.0.5-4)计算。现在要问,当按受冲切承载力计算时,基础高度与下列哪一数值最接近?A.600mmB.750mmC.700mmD.800mm
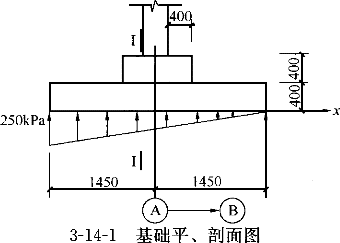
- 设图3-14-1中的基础阶高H=400mm,基础底面所受的相应于荷载效应标准组合的地基净反力标准值为250kPa。配筋计算时,内力臂取用0.9h
 ,a
,a =60mm。问当按受弯承载力计算时,其沿Y方向与沿X方向的布置配筋,下列哪一组数值最为接近?
=60mm。问当按受弯承载力计算时,其沿Y方向与沿X方向的布置配筋,下列哪一组数值最为接近?
 A.2018mm
A.2018mm ,1096mm
,1096mm B.2018mm
B.2018mm ,1740mm
,1740mm C.2550mm
C.2550mm ,2550mm
,2550mm D.1740mm
D.1740mm ,1740mm
,1740mm
正确答案:
(1)B
(2)C
(2)C
答案解析:
第1小题:【主要解答过程如下】:(1)根据《建筑地基基础设计规范》8.2.7条,对矩形截面柱的矩形基础,应验算柱与基础交接处以及基础变阶处的受冲切承载力。受冲切承载力应符合下式要求:
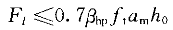 (3-13-1)
(3-13-1)
F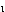 ≤p
≤p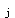 A
A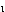 (3-13-2)
(3-13-2)
式中β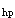 --受冲切承载力截面高度影响系数,当h不大于800mm时,取1.0;
--受冲切承载力截面高度影响系数,当h不大于800mm时,取1.0;
A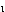 --冲切验算时取用的部分基底面积,即图313-1中阴影所示面积;
--冲切验算时取用的部分基底面积,即图313-1中阴影所示面积;
n --冲切破坏锥体最不利一侧计算长度;
--冲切破坏锥体最不利一侧计算长度;
p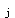 --相应于荷载效应基本组合的地基土单位面积净反力。
--相应于荷载效应基本组合的地基土单位面积净反力。
(2)柱与基础交接处的受冲切承载力
已知p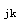 =300kPa=0.3N/mm
=300kPa=0.3N/mm ,P
,P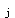 =1.35×0.3=0.405N/mm
=1.35×0.3=0.405N/mm
h =H+H-60=2H-60
=H+H-60=2H-60
A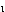 =(1/2)×(1235-2H)(29004-4304-4H)
=(1/2)×(1235-2H)(29004-4304-4H)
=(1235-2H)(1665+2H)=2056275-860H-4H
依据地基规范公式(3.0.5-4)
F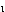 =0.405×(2056275-860H-4H
=0.405×(2056275-860H-4H )
)
=832791-348H-1.62H
a =(550+4304-4H)×(1/2)=4904-2H
=(550+4304-4H)×(1/2)=4904-2H
设基础总高度h≤800mm,β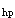 =1.0,将上述数值代入式(3-13-1)得:
=1.0,将上述数值代入式(3-13-1)得:
832791-348H-1.62H =0.7×1.0×1.43×(490+2H)×(2H-60)
=0.7×1.0×1.43×(490+2H)×(2H-60)
=860H4-4H -29400
-29400
化简后有:H +215H-153415=0
+215H-153415=0
H=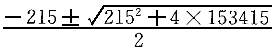 =298.5mm
=298.5mm
(3)基础变阶处的受冲切承载力
h =H-60
=H-60
F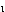 =832791-348H-1.62H
=832791-348H-1.62H
a =(550+2H+430+4H)×(1/2)=490+3H
=(550+2H+430+4H)×(1/2)=490+3H
设h≤800mm,β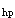 =1.0,将上述数值代入式(3-13-1):
=1.0,将上述数值代入式(3-13-1):
832791-348H-1.62H =0.7×1.0×1.43×(490+3H)(H-60)
=0.7×1.0×1.43×(490+3H)(H-60)
=3H +310H-29400
+310H-29400
化简后得到:H +142H-186621=0
+142H-186621=0
H= =367mm>298.5mm
=367mm>298.5mm
因此基础高度h=2H=367×2=734mm,取用750mm,此即选项B。A系按柱与基础交接处的受冲切承载力得到,并非最不利情况;C是荷载分项系数错误地取用1.20所致;D则荷载分项系数采用了1.40。
【点评】:(1)本题是最简单的钢筋混凝土矩形截面柱下独立基础受冲切承载力计算,规范中有完整的计算方法,考生应熟练地掌握。对于圆形截面柱,应换算为方形截面,换算截面的边长取圆形截面直径的0.8倍(见《钢筋混凝土承台设计规程》(CECS88:97)4.2.8条)。
(2)关于柱对平板式筏基的受冲切承载力计算,则较为复杂。《混凝土结构设计规范》公式(7.7.1-1)给出了在局部荷载或集中反力作用下的受冲切承载力计算公式:
 (3-13-3)
(3-13-3)
式中,β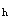 即式(3-13-1)中的β
即式(3-13-1)中的β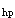 ;F
;F 为等效集中反力设计值,按7.7.5条计算:η见规范7.7.1条;μ
为等效集中反力设计值,按7.7.5条计算:η见规范7.7.1条;μ 为临界截面的周长,即距离局部荷载或集中反力作用面积周边h
为临界截面的周长,即距离局部荷载或集中反力作用面积周边h /2处的板垂直截面的最不利周长。应该指出,根据7.7.1~7.7.2条条文说明,对非矩形截面柱(异形截面柱)的临界截面周长,宜选取周长u
/2处的板垂直截面的最不利周长。应该指出,根据7.7.1~7.7.2条条文说明,对非矩形截面柱(异形截面柱)的临界截面周长,宜选取周长u 的形状要呈凸形折线,其折角不能大于180°,由此可得到最不利周长,此时在局部周长区段离柱边的距离允许大于h
的形状要呈凸形折线,其折角不能大于180°,由此可得到最不利周长,此时在局部周长区段离柱边的距离允许大于h /2。图3-13-2列出了一些典型情况,可供读者参考。
/2。图3-13-2列出了一些典型情况,可供读者参考。

(3)截面高度影响系数β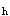 (β
(β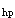 )
)
根据《混凝土结构设计规范》7.7。1条,β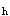 的取值:当h≤800mm时,取1.0;当h≥2000mm时,取0.9,其间按线性内插法取用。尺寸效应问题,国内试验资料不多,多是根据国外试验资料,且这些试验资料都是无腹筋梁的资料。试验的结果表明随梁有效高度的增加,无腹筋梁受剪承载力降低。理论与试验研究还证明,纵筋沿梁高分层布置时,层间距较之截面有效高度h
的取值:当h≤800mm时,取1.0;当h≥2000mm时,取0.9,其间按线性内插法取用。尺寸效应问题,国内试验资料不多,多是根据国外试验资料,且这些试验资料都是无腹筋梁的资料。试验的结果表明随梁有效高度的增加,无腹筋梁受剪承载力降低。理论与试验研究还证明,纵筋沿梁高分层布置时,层间距较之截面有效高度h 的影响更为显著,M.P.Collins在试验的基础上提出了一个计算混凝土受剪承载力的计算公式:
的影响更为显著,M.P.Collins在试验的基础上提出了一个计算混凝土受剪承载力的计算公式:
V =245/1275+S
=245/1275+S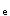 (
(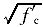 bh
bh );S
);S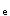 =35S
=35S a+16
a+16
式中a--骨料最大尺寸;
S --纵向钢筋沿梁的间距。
--纵向钢筋沿梁的间距。
当沿梁高不另加纵向钢筋时,S =0.9h
=0.9h ,S
,S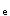 =31.5h
=31.5h /a+16;
/a+16;
当沿梁高另加一层纵向钢筋时,S =0.45h
=0.45h
S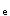 =15.75h
=15.75h a+16
a+16
将其分别代入V 的公式,显然后者较前者的受剪承载力提高了,这是因为梁腹分布布置纵向钢筋可以有效地约束斜裂缝发展。基础平板受冲切属于双向剪切,因此上述有关梁剪的讨论,对厚板受冲切同样有效。规范10.1.11条规定,对基础筏板,当板厚h>2m时,除应沿上、下表面布置纵、横方向的钢筋外,尚宜沿板厚度方向间距不超过1m设置与板面平行的构造网片,这不仅是构造的需要,如上所述还有利于抗剪和抗冲切,请考生注意。
的公式,显然后者较前者的受剪承载力提高了,这是因为梁腹分布布置纵向钢筋可以有效地约束斜裂缝发展。基础平板受冲切属于双向剪切,因此上述有关梁剪的讨论,对厚板受冲切同样有效。规范10.1.11条规定,对基础筏板,当板厚h>2m时,除应沿上、下表面布置纵、横方向的钢筋外,尚宜沿板厚度方向间距不超过1m设置与板面平行的构造网片,这不仅是构造的需要,如上所述还有利于抗剪和抗冲切,请考生注意。
第2小题:【主要解答过程如下】:(1)根据《建筑地基基础设计规范》公式(8.2.7-4)计算基础底部沿Y方向布置的纵向受力钢筋截面面积。当取净反力设计值时,公式简化为:
 (3-14-1)
(3-14-1)
式中p =1.35×250=337.5kPa,p
=1.35×250=337.5kPa,p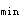 =0
=0
p--柱边处及基础变阶处地基净反力设计值按图3-14-2计算。

①柱边处
M′ =(1/12)×(1.45-0.275)
=(1/12)×(1.45-0.275) ×[(2×2.9+0.55)×(337.5+200.75)+(337.5-200.75)×2.9]=438.86kN·m
×[(2×2.9+0.55)×(337.5+200.75)+(337.5-200.75)×2.9]=438.86kN·m
h =800-60=740mm
=800-60=740mm
 =438.86×10
=438.86×10 /0.9×740×360=1830mm
/0.9×740×360=1830mm
根据《混凝土结构设计规范》9.5.2条,基础配筋率不应小于0.15%,因此纵向受力钢筋构造配筋的面积为:(400×2900+1350×400)×(0.15/100)=2550mm >1830mm
>1830mm 。
。
②基础变阶处
M″ =(1/12)×(1.45-0.675)
=(1/12)×(1.45-0.675) ×[(2×2.9+1.35)×(337.5+247.3)+(337.5-247.3)×2.9]=222.38kN·m
×[(2×2.9+1.35)×(337.5+247.3)+(337.5-247.3)×2.9]=222.38kN·m
h =400-60=340mm
=400-60=340mm
A″ =222.38×10
=222.38×10 /0.9×340×360=2018.7mm
/0.9×340×360=2018.7mm <2550mm
<2550mm
故沿Y方向布置所需的纵向钢筋面积应为2550mm 。
。
(2)根据地基规范公式(8.2.7-5)计算基础底部沿X方向布置的纵向受力钢筋截面面积。当取净反力值时公式简化为:
M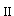 =1/48(ι-a′)
=1/48(ι-a′) (2b+b′)(p
(2b+b′)(p -p
-p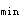 )(3-14-2)
)(3-14-2)
①柱边处
M′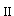 =1/48(2.9-0.55)
=1/48(2.9-0.55) ×(2×2.9+0.55)×337.5=246.57kN·m
×(2×2.9+0.55)×337.5=246.57kN·m
A′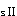 =246.57×10
=246.57×10 /0.9×740×360=1028mm
/0.9×740×360=1028mm <2550mm
<2550mm
②基础变阶处
M″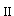 =1/48×(2.9-1.35)
=1/48×(2.9-1.35) ×(2×2.9+1.35)×337.5=120.78kN·m
×(2×2.9+1.35)×337.5=120.78kN·m
A″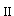 =120.78×10
=120.78×10 /0.9×340×360=1096mm
/0.9×340×360=1096mm <2550mm
<2550mm
因此依据上面计算得知,沿Y方向及沿X方向布置的钢筋均应为2550mm ,与选项C相符。选项A为按计算配筋,不符合满足最小配筋率的要求;选项B、D中1740mm
,与选项C相符。选项A为按计算配筋,不符合满足最小配筋率的要求;选项B、D中1740mm 是按下台阶的最小配筋率计算,为不正确选项。
是按下台阶的最小配筋率计算,为不正确选项。
【点评】:(1)本题是矩形基础的受弯承载力计算,规范中亦有完整的计算公式。其中关键问题是根据最小配筋率0.15%计算受拉钢筋面积时应取哪一个截面面积。众所周知,最小配筋率p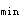 为少筋梁与适筋梁的界限,p
为少筋梁与适筋梁的界限,p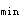 可按钢筋混凝土梁正截面的极限弯矩等于同样截面、同一混凝土强度等级的素混凝土梁的正截面极限弯矩(即开裂弯矩M
可按钢筋混凝土梁正截面的极限弯矩等于同样截面、同一混凝土强度等级的素混凝土梁的正截面极限弯矩(即开裂弯矩M )的条件确定。
)的条件确定。
对于矩形截面素混凝土梁,M =0.292f
=0.292f bh
bh ;M
;M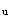 =ρ
=ρ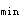 bh
bh f
f (h
(h -0.5x),令两式相等,并取h
-0.5x),令两式相等,并取h -0.5x≈0.95h
-0.5x≈0.95h 及h≈1.05h
及h≈1.05h ,即可得到:
,即可得到:
ρ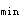 =0.35(f
=0.35(f /f
/f ),A
),A =ρ
=ρ bh
bh
从上述推导过程得知,计算最小受拉钢筋面积时应取计算弯矩截面,在此即为柱边截面。
但计算最小受拉钢筋面积时,截面高度似应取有效高度,而不应取全高。但根据规范表9.5.1的表注规定,受弯构件的最小配筋应按全截面面积计算。为此本题采用了按基础全截面面积计算最小受拉钢筋截面面积。
(2)美国规范AC1318-2004规定:当实际纵向钢筋配筋率超过计算所需配筋率至少1/3时,可不受最小配筋率的限制,可供读者参考。
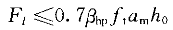 (3-13-1)
(3-13-1)F
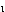 ≤p
≤p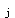 A
A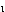 (3-13-2)
(3-13-2)式中β
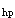 --受冲切承载力截面高度影响系数,当h不大于800mm时,取1.0;
--受冲切承载力截面高度影响系数,当h不大于800mm时,取1.0;A
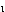 --冲切验算时取用的部分基底面积,即图313-1中阴影所示面积;
--冲切验算时取用的部分基底面积,即图313-1中阴影所示面积;n
 --冲切破坏锥体最不利一侧计算长度;
--冲切破坏锥体最不利一侧计算长度;p
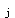 --相应于荷载效应基本组合的地基土单位面积净反力。
--相应于荷载效应基本组合的地基土单位面积净反力。(2)柱与基础交接处的受冲切承载力
已知p
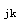 =300kPa=0.3N/mm
=300kPa=0.3N/mm ,P
,P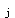 =1.35×0.3=0.405N/mm
=1.35×0.3=0.405N/mm
h
 =H+H-60=2H-60
=H+H-60=2H-60A
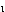 =(1/2)×(1235-2H)(29004-4304-4H)
=(1/2)×(1235-2H)(29004-4304-4H)=(1235-2H)(1665+2H)=2056275-860H-4H

依据地基规范公式(3.0.5-4)
F
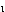 =0.405×(2056275-860H-4H
=0.405×(2056275-860H-4H )
)=832791-348H-1.62H

a
 =(550+4304-4H)×(1/2)=4904-2H
=(550+4304-4H)×(1/2)=4904-2H设基础总高度h≤800mm,β
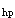 =1.0,将上述数值代入式(3-13-1)得:
=1.0,将上述数值代入式(3-13-1)得:832791-348H-1.62H
 =0.7×1.0×1.43×(490+2H)×(2H-60)
=0.7×1.0×1.43×(490+2H)×(2H-60)=860H4-4H
 -29400
-29400化简后有:H
 +215H-153415=0
+215H-153415=0H=
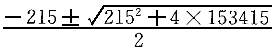 =298.5mm
=298.5mm(3)基础变阶处的受冲切承载力
h
 =H-60
=H-60F
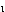 =832791-348H-1.62H
=832791-348H-1.62H
a
 =(550+2H+430+4H)×(1/2)=490+3H
=(550+2H+430+4H)×(1/2)=490+3H设h≤800mm,β
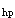 =1.0,将上述数值代入式(3-13-1):
=1.0,将上述数值代入式(3-13-1):832791-348H-1.62H
 =0.7×1.0×1.43×(490+3H)(H-60)
=0.7×1.0×1.43×(490+3H)(H-60)=3H
 +310H-29400
+310H-29400化简后得到:H
 +142H-186621=0
+142H-186621=0H=
 =367mm>298.5mm
=367mm>298.5mm因此基础高度h=2H=367×2=734mm,取用750mm,此即选项B。A系按柱与基础交接处的受冲切承载力得到,并非最不利情况;C是荷载分项系数错误地取用1.20所致;D则荷载分项系数采用了1.40。
【点评】:(1)本题是最简单的钢筋混凝土矩形截面柱下独立基础受冲切承载力计算,规范中有完整的计算方法,考生应熟练地掌握。对于圆形截面柱,应换算为方形截面,换算截面的边长取圆形截面直径的0.8倍(见《钢筋混凝土承台设计规程》(CECS88:97)4.2.8条)。
(2)关于柱对平板式筏基的受冲切承载力计算,则较为复杂。《混凝土结构设计规范》公式(7.7.1-1)给出了在局部荷载或集中反力作用下的受冲切承载力计算公式:
 (3-13-3)
(3-13-3)式中,β
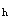 即式(3-13-1)中的β
即式(3-13-1)中的β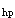 ;F
;F 为等效集中反力设计值,按7.7.5条计算:η见规范7.7.1条;μ
为等效集中反力设计值,按7.7.5条计算:η见规范7.7.1条;μ 为临界截面的周长,即距离局部荷载或集中反力作用面积周边h
为临界截面的周长,即距离局部荷载或集中反力作用面积周边h /2处的板垂直截面的最不利周长。应该指出,根据7.7.1~7.7.2条条文说明,对非矩形截面柱(异形截面柱)的临界截面周长,宜选取周长u
/2处的板垂直截面的最不利周长。应该指出,根据7.7.1~7.7.2条条文说明,对非矩形截面柱(异形截面柱)的临界截面周长,宜选取周长u 的形状要呈凸形折线,其折角不能大于180°,由此可得到最不利周长,此时在局部周长区段离柱边的距离允许大于h
的形状要呈凸形折线,其折角不能大于180°,由此可得到最不利周长,此时在局部周长区段离柱边的距离允许大于h /2。图3-13-2列出了一些典型情况,可供读者参考。
/2。图3-13-2列出了一些典型情况,可供读者参考。
(3)截面高度影响系数β
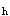 (β
(β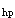 )
)根据《混凝土结构设计规范》7.7。1条,β
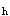 的取值:当h≤800mm时,取1.0;当h≥2000mm时,取0.9,其间按线性内插法取用。尺寸效应问题,国内试验资料不多,多是根据国外试验资料,且这些试验资料都是无腹筋梁的资料。试验的结果表明随梁有效高度的增加,无腹筋梁受剪承载力降低。理论与试验研究还证明,纵筋沿梁高分层布置时,层间距较之截面有效高度h
的取值:当h≤800mm时,取1.0;当h≥2000mm时,取0.9,其间按线性内插法取用。尺寸效应问题,国内试验资料不多,多是根据国外试验资料,且这些试验资料都是无腹筋梁的资料。试验的结果表明随梁有效高度的增加,无腹筋梁受剪承载力降低。理论与试验研究还证明,纵筋沿梁高分层布置时,层间距较之截面有效高度h 的影响更为显著,M.P.Collins在试验的基础上提出了一个计算混凝土受剪承载力的计算公式:
的影响更为显著,M.P.Collins在试验的基础上提出了一个计算混凝土受剪承载力的计算公式:V
 =245/1275+S
=245/1275+S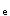 (
(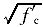 bh
bh );S
);S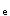 =35S
=35S a+16
a+16式中a--骨料最大尺寸;
S
 --纵向钢筋沿梁的间距。
--纵向钢筋沿梁的间距。当沿梁高不另加纵向钢筋时,S
 =0.9h
=0.9h ,S
,S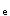 =31.5h
=31.5h /a+16;
/a+16;当沿梁高另加一层纵向钢筋时,S
 =0.45h
=0.45h
S
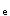 =15.75h
=15.75h a+16
a+16将其分别代入V
 的公式,显然后者较前者的受剪承载力提高了,这是因为梁腹分布布置纵向钢筋可以有效地约束斜裂缝发展。基础平板受冲切属于双向剪切,因此上述有关梁剪的讨论,对厚板受冲切同样有效。规范10.1.11条规定,对基础筏板,当板厚h>2m时,除应沿上、下表面布置纵、横方向的钢筋外,尚宜沿板厚度方向间距不超过1m设置与板面平行的构造网片,这不仅是构造的需要,如上所述还有利于抗剪和抗冲切,请考生注意。
的公式,显然后者较前者的受剪承载力提高了,这是因为梁腹分布布置纵向钢筋可以有效地约束斜裂缝发展。基础平板受冲切属于双向剪切,因此上述有关梁剪的讨论,对厚板受冲切同样有效。规范10.1.11条规定,对基础筏板,当板厚h>2m时,除应沿上、下表面布置纵、横方向的钢筋外,尚宜沿板厚度方向间距不超过1m设置与板面平行的构造网片,这不仅是构造的需要,如上所述还有利于抗剪和抗冲切,请考生注意。第2小题:【主要解答过程如下】:(1)根据《建筑地基基础设计规范》公式(8.2.7-4)计算基础底部沿Y方向布置的纵向受力钢筋截面面积。当取净反力设计值时,公式简化为:
 (3-14-1)
(3-14-1)式中p
 =1.35×250=337.5kPa,p
=1.35×250=337.5kPa,p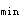 =0
=0p--柱边处及基础变阶处地基净反力设计值按图3-14-2计算。

①柱边处
M′
 =(1/12)×(1.45-0.275)
=(1/12)×(1.45-0.275) ×[(2×2.9+0.55)×(337.5+200.75)+(337.5-200.75)×2.9]=438.86kN·m
×[(2×2.9+0.55)×(337.5+200.75)+(337.5-200.75)×2.9]=438.86kN·mh
 =800-60=740mm
=800-60=740mm =438.86×10
=438.86×10 /0.9×740×360=1830mm
/0.9×740×360=1830mm
根据《混凝土结构设计规范》9.5.2条,基础配筋率不应小于0.15%,因此纵向受力钢筋构造配筋的面积为:(400×2900+1350×400)×(0.15/100)=2550mm
 >1830mm
>1830mm 。
。②基础变阶处
M″
 =(1/12)×(1.45-0.675)
=(1/12)×(1.45-0.675) ×[(2×2.9+1.35)×(337.5+247.3)+(337.5-247.3)×2.9]=222.38kN·m
×[(2×2.9+1.35)×(337.5+247.3)+(337.5-247.3)×2.9]=222.38kN·mh
 =400-60=340mm
=400-60=340mmA″
 =222.38×10
=222.38×10 /0.9×340×360=2018.7mm
/0.9×340×360=2018.7mm <2550mm
<2550mm
故沿Y方向布置所需的纵向钢筋面积应为2550mm
 。
。(2)根据地基规范公式(8.2.7-5)计算基础底部沿X方向布置的纵向受力钢筋截面面积。当取净反力值时公式简化为:
M
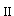 =1/48(ι-a′)
=1/48(ι-a′) (2b+b′)(p
(2b+b′)(p -p
-p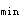 )(3-14-2)
)(3-14-2)①柱边处
M′
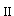 =1/48(2.9-0.55)
=1/48(2.9-0.55) ×(2×2.9+0.55)×337.5=246.57kN·m
×(2×2.9+0.55)×337.5=246.57kN·mA′
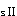 =246.57×10
=246.57×10 /0.9×740×360=1028mm
/0.9×740×360=1028mm <2550mm
<2550mm
②基础变阶处
M″
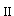 =1/48×(2.9-1.35)
=1/48×(2.9-1.35) ×(2×2.9+1.35)×337.5=120.78kN·m
×(2×2.9+1.35)×337.5=120.78kN·mA″
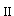 =120.78×10
=120.78×10 /0.9×340×360=1096mm
/0.9×340×360=1096mm <2550mm
<2550mm
因此依据上面计算得知,沿Y方向及沿X方向布置的钢筋均应为2550mm
 ,与选项C相符。选项A为按计算配筋,不符合满足最小配筋率的要求;选项B、D中1740mm
,与选项C相符。选项A为按计算配筋,不符合满足最小配筋率的要求;选项B、D中1740mm 是按下台阶的最小配筋率计算,为不正确选项。
是按下台阶的最小配筋率计算,为不正确选项。【点评】:(1)本题是矩形基础的受弯承载力计算,规范中亦有完整的计算公式。其中关键问题是根据最小配筋率0.15%计算受拉钢筋面积时应取哪一个截面面积。众所周知,最小配筋率p
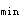 为少筋梁与适筋梁的界限,p
为少筋梁与适筋梁的界限,p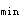 可按钢筋混凝土梁正截面的极限弯矩等于同样截面、同一混凝土强度等级的素混凝土梁的正截面极限弯矩(即开裂弯矩M
可按钢筋混凝土梁正截面的极限弯矩等于同样截面、同一混凝土强度等级的素混凝土梁的正截面极限弯矩(即开裂弯矩M )的条件确定。
)的条件确定。对于矩形截面素混凝土梁,M
 =0.292f
=0.292f bh
bh ;M
;M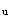 =ρ
=ρ bh
bh f
f (h
(h -0.5x),令两式相等,并取h
-0.5x),令两式相等,并取h -0.5x≈0.95h
-0.5x≈0.95h 及h≈1.05h
及h≈1.05h ,即可得到:
,即可得到:ρ
 =0.35(f
=0.35(f /f
/f ),A
),A =ρ
=ρ bh
bh
从上述推导过程得知,计算最小受拉钢筋面积时应取计算弯矩截面,在此即为柱边截面。
但计算最小受拉钢筋面积时,截面高度似应取有效高度,而不应取全高。但根据规范表9.5.1的表注规定,受弯构件的最小配筋应按全截面面积计算。为此本题采用了按基础全截面面积计算最小受拉钢筋截面面积。
(2)美国规范AC1318-2004规定:当实际纵向钢筋配筋率超过计算所需配筋率至少1/3时,可不受最小配筋率的限制,可供读者参考。
