某11层钢筋混凝土框架结构,抗震设防烈度为8度,Ⅲ类场地,设计地震分组为一组,层高均为3.6m,刚度较均匀,采用轻质隔墙,按弹性方法计算罕遇地震作用下底层层间位移△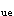 =8.5mm,楼层服强度系数ξ
=8.5mm,楼层服强度系数ξ =0.4(提示:此值不小于相邻层平均ξ
=0.4(提示:此值不小于相邻层平均ξ 值的80%),问罕遇地震作用下层间弹塑性位移计算结果,与下列何项数值最接近?
值的80%),问罕遇地震作用下层间弹塑性位移计算结果,与下列何项数值最接近?
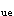 =8.5mm,楼层服强度系数ξ
=8.5mm,楼层服强度系数ξ =0.4(提示:此值不小于相邻层平均ξ
=0.4(提示:此值不小于相邻层平均ξ 值的80%),问罕遇地震作用下层间弹塑性位移计算结果,与下列何项数值最接近?
值的80%),问罕遇地震作用下层间弹塑性位移计算结果,与下列何项数值最接近? 正确答案:
B
答案解析:
【主要解答过程如下】:根据《高规》第5.5.3条规定,层间弹塑性位移可按公式(5.5.3-1)计算,当薄弱层屈服强度系数ξ 不小于相邻层平均ξ
不小于相邻层平均ξ 值的80%时,可按表5.5.3求η
值的80%时,可按表5.5.3求η 。
。
查表5.5.3,当ξ =0.4时,得η
=0.4时,得η =2.0。
=2.0。
故有△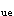 =η
=η △
△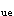 =2.0×8.5=17.0mm,与选项B相符。
=2.0×8.5=17.0mm,与选项B相符。
【点评】:(1)钢筋混凝土框架结构及高大单层钢筋混凝土柱厂房等结构,在大地震中往往受到严重甚至倒塌。实际震害分析及实验研究表明,除了这些结构刚度相对较小而变形较大外,更主要的是存在承载力验算所没有发现的薄弱部位--其承载力本身虽满足设计地震作用下抗震承载力的要求,却比相邻部位薄弱得多。对于单层厂房,这种破坏多发生在8度Ⅲ、Ⅳ类场地和9度区,破坏部位是上柱,因为上柱的承载力一般相对较小且其下端的支承条件不如下柱。对于底部框架-抗震墙结构,则底部是明显的薄弱部位。
目前各国规范的变形估计公式有三种:一是按假想的完全弹性体计算;二是将额定地震作用下的弹性变形乘以放大系数,即△ =η
=η △
△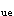 ;三是按时程分析法等专门程序计算。
;三是按时程分析法等专门程序计算。
其中采用第二种的最多,我国规范也采用第二种方法,《高规》第5.5.3条规定:
结构薄弱层(部位)层间弹塑性位移的简化计算,宜符合下列要求:
①结构薄弱层(部位)的位置可按下列情况确定:
a.楼层屈服强度系数沿高度分布均匀的结构,可取底层;
b.楼层屈服强度系数沿高度分布不均匀的结构,可取该系数最小的楼层(部位)及相对较小的楼层,一般不超过2~3处。
②层间弹塑性位移可按下列公式计算:
△ =η
=η △
△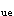 (5.5.3-1)
(5.5.3-1)
或△ =μ△
=μ△ =(η
=(η ξ
ξ )△
)△ (5.5.3-2)
(5.5.3-2)
式中△ --层间弹塑性位移;
--层间弹塑性位移;
△ --层间屈服位移;
--层间屈服位移;
μ--楼层延性系数;
△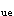 一罕遇地震作用下按弹性分析的层间位移。计算时,水平地震影响系数最大值应按《高规》表3.3.7-1采用;
一罕遇地震作用下按弹性分析的层间位移。计算时,水平地震影响系数最大值应按《高规》表3.3.7-1采用;
η --弹塑性位移增大系数,当薄弱层(部位)的屈服强度系数不小于相邻层(部分)该系数平均值的0.8时,可按表5.5.3采用;当不大于该平均值的0.5时,可按表内相应数值的1.5倍采用;其他情况可采用内插法取值;
--弹塑性位移增大系数,当薄弱层(部位)的屈服强度系数不小于相邻层(部分)该系数平均值的0.8时,可按表5.5.3采用;当不大于该平均值的0.5时,可按表内相应数值的1.5倍采用;其他情况可采用内插法取值;
ξ --楼层屈服强度系数。
--楼层屈服强度系数。

(2)值得注意的是:对于屈服强度系数ξ 均匀的多层结构,其最大的层间弹塑变形增大系数η
均匀的多层结构,其最大的层间弹塑变形增大系数η 可按层数和的£差异表格形式给出;对于ξ
可按层数和的£差异表格形式给出;对于ξ 不均匀的结构,其情况复杂,在弹性刚度沿高度变化较平缓时,可近似用均匀结构的η
不均匀的结构,其情况复杂,在弹性刚度沿高度变化较平缓时,可近似用均匀结构的η 适当放大取值;对其他情况,一般需要用静力弹塑性分析、弹塑性时程分析法或内力重分布法等予以估计。所以,题中楼层屈服强度系数ξ[y.gif不小于相邻层平均ξ[y.gif值的80%的提示,是非常必要的。
适当放大取值;对其他情况,一般需要用静力弹塑性分析、弹塑性时程分析法或内力重分布法等予以估计。所以,题中楼层屈服强度系数ξ[y.gif不小于相邻层平均ξ[y.gif值的80%的提示,是非常必要的。
 不小于相邻层平均ξ
不小于相邻层平均ξ 值的80%时,可按表5.5.3求η
值的80%时,可按表5.5.3求η 。
。查表5.5.3,当ξ
 =0.4时,得η
=0.4时,得η =2.0。
=2.0。故有△
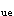 =η
=η △
△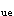 =2.0×8.5=17.0mm,与选项B相符。
=2.0×8.5=17.0mm,与选项B相符。【点评】:(1)钢筋混凝土框架结构及高大单层钢筋混凝土柱厂房等结构,在大地震中往往受到严重甚至倒塌。实际震害分析及实验研究表明,除了这些结构刚度相对较小而变形较大外,更主要的是存在承载力验算所没有发现的薄弱部位--其承载力本身虽满足设计地震作用下抗震承载力的要求,却比相邻部位薄弱得多。对于单层厂房,这种破坏多发生在8度Ⅲ、Ⅳ类场地和9度区,破坏部位是上柱,因为上柱的承载力一般相对较小且其下端的支承条件不如下柱。对于底部框架-抗震墙结构,则底部是明显的薄弱部位。
目前各国规范的变形估计公式有三种:一是按假想的完全弹性体计算;二是将额定地震作用下的弹性变形乘以放大系数,即△
 =η
=η △
△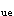 ;三是按时程分析法等专门程序计算。
;三是按时程分析法等专门程序计算。其中采用第二种的最多,我国规范也采用第二种方法,《高规》第5.5.3条规定:
结构薄弱层(部位)层间弹塑性位移的简化计算,宜符合下列要求:
①结构薄弱层(部位)的位置可按下列情况确定:
a.楼层屈服强度系数沿高度分布均匀的结构,可取底层;
b.楼层屈服强度系数沿高度分布不均匀的结构,可取该系数最小的楼层(部位)及相对较小的楼层,一般不超过2~3处。
②层间弹塑性位移可按下列公式计算:
△
 =η
=η △
△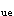 (5.5.3-1)
(5.5.3-1)或△
 =μ△
=μ△ =(η
=(η ξ
ξ )△
)△ (5.5.3-2)
(5.5.3-2)式中△
 --层间弹塑性位移;
--层间弹塑性位移;△
 --层间屈服位移;
--层间屈服位移;μ--楼层延性系数;
△
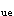 一罕遇地震作用下按弹性分析的层间位移。计算时,水平地震影响系数最大值应按《高规》表3.3.7-1采用;
一罕遇地震作用下按弹性分析的层间位移。计算时,水平地震影响系数最大值应按《高规》表3.3.7-1采用;η
 --弹塑性位移增大系数,当薄弱层(部位)的屈服强度系数不小于相邻层(部分)该系数平均值的0.8时,可按表5.5.3采用;当不大于该平均值的0.5时,可按表内相应数值的1.5倍采用;其他情况可采用内插法取值;
--弹塑性位移增大系数,当薄弱层(部位)的屈服强度系数不小于相邻层(部分)该系数平均值的0.8时,可按表5.5.3采用;当不大于该平均值的0.5时,可按表内相应数值的1.5倍采用;其他情况可采用内插法取值;ξ
 --楼层屈服强度系数。
--楼层屈服强度系数。
(2)值得注意的是:对于屈服强度系数ξ
 均匀的多层结构,其最大的层间弹塑变形增大系数η
均匀的多层结构,其最大的层间弹塑变形增大系数η 可按层数和的£差异表格形式给出;对于ξ
可按层数和的£差异表格形式给出;对于ξ 不均匀的结构,其情况复杂,在弹性刚度沿高度变化较平缓时,可近似用均匀结构的η
不均匀的结构,其情况复杂,在弹性刚度沿高度变化较平缓时,可近似用均匀结构的η 适当放大取值;对其他情况,一般需要用静力弹塑性分析、弹塑性时程分析法或内力重分布法等予以估计。所以,题中楼层屈服强度系数ξ[y.gif不小于相邻层平均ξ[y.gif值的80%的提示,是非常必要的。
适当放大取值;对其他情况,一般需要用静力弹塑性分析、弹塑性时程分析法或内力重分布法等予以估计。所以,题中楼层屈服强度系数ξ[y.gif不小于相邻层平均ξ[y.gif值的80%的提示,是非常必要的。