某管道支架横梁,截面尺寸为b×h=200mm×400mm;混凝土强度等级C25,主筋采用HRB335级钢筋;因为在风荷载作用下梁承受的变号弯矩数值相同,梁自重弯矩很小,故采用对称配筋,上、下各2 20;非抗震设计,r
20;非抗震设计,r =1.0,a
=1.0,a =a′
=a′ =40mm。则在竖向荷载作用下,下列弯矩值的哪一个与此截面所能承受的弯矩值最接近?
=40mm。则在竖向荷载作用下,下列弯矩值的哪一个与此截面所能承受的弯矩值最接近?
 20;非抗震设计,r
20;非抗震设计,r =1.0,a
=1.0,a =a′
=a′ =40mm。则在竖向荷载作用下,下列弯矩值的哪一个与此截面所能承受的弯矩值最接近?
=40mm。则在竖向荷载作用下,下列弯矩值的哪一个与此截面所能承受的弯矩值最接近? 正确答案:
A
答案解析:
【主要解答过程如下】:(1)解法1
在对称配筋情况下,受压钢筋应力不可能达到f′ 。此时某钢筋应力可按《混凝土结构设计规范》公式(7.1.5-1)计算:
。此时某钢筋应力可按《混凝土结构设计规范》公式(7.1.5-1)计算:
 (3-15-1)
(3-15-1)
式中,h′ 为纵向受压钢筋截面重心至截面受压边缘的距离,h′
为纵向受压钢筋截面重心至截面受压边缘的距离,h′ =a′
=a′ =40mm。
=40mm。
σ′ =2.0×10
=2.0×10 ×0.0033×[(0.8×40/x)-1]=660[(32/x)-1]
×0.0033×[(0.8×40/x)-1]=660[(32/x)-1]
根据内力平衡条件可以写出:
 (3-15-2)
(3-15-2)
1.0×11.9×200x=300×628+660[(32/x)-1]×628
化简后得到
x +95x-5573=0
+95x-5573=0
x= =41mm
=41mm
σ′ =660[(32/41)-1]=-145N/mm
=660[(32/41)-1]=-145N/mm
根据对A 取矩的平衡关系:
取矩的平衡关系:
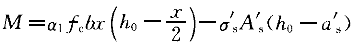 (3-15-3)
(3-15-3)
=1.0×11.9×200×41×(360-41/2)+145×628×(360-40)
=62267610N·mm=62.268kN·m
(2)解法2
受压钢筋的应力按规范近似公式(7.1.5-3)计算:
 (3-15-4)
(3-15-4)
式中

于是
σ′ =300/0.55-0.8[(x/40)-0.8]=-30x+960
=300/0.55-0.8[(x/40)-0.8]=-30x+960
根据式(3-15-2)
1.0×11.9×200x=300×628+(-30x+960)×628
σ′ =-30×37.3+960=-159N/mm
=-30×37.3+960=-159N/mm
又从式(3-15-3)得:
M=1.0×11.9×200×37.3×[360-(1/2)×37.3]+159×628×320
=62255644N·mm=62.256kN·m
(3)解法3
按近似方法计算,取x=2a′ =80mm
=80mm
M=300×628×320=60288000N·mm=60.288kN·m
从以上计算结果可以看出,解法1与解法2所得的弯矩值基本相同,说明了采用近似公式(3-15-4)计算钢筋应力的合理性;解法3虽弯矩值略有差异,但与解法1相比,其误差只有3.18%,可以接受,所以按上述三种方法计算都是合理的,选项A是正确的。
选项B则是错误地取用f =360N/mm
=360N/mm 计算所得结果,选项C系按水平梁计算,选项D是计算错误,都是不正确的。
计算所得结果,选项C系按水平梁计算,选项D是计算错误,都是不正确的。
【点评】:公式(3-15-1)是根据中和轴高度等于x/β 、混凝土极限压应变ε
、混凝土极限压应变ε ,按平截面假定导出的求钢筋应力的一般公式。为了简化计算,避免在正截面承载力计算中出现求解二次方程,根据试验资料的分析,考虑到ξ=ξ
,按平截面假定导出的求钢筋应力的一般公式。为了简化计算,避免在正截面承载力计算中出现求解二次方程,根据试验资料的分析,考虑到ξ=ξ 及ξ=β
及ξ=β 的边界条件,σ
的边界条件,σ 与x/h
与x/h 可采用近似的线性关系,即公式(3-15-4)。按上述两个公式可以计算截面任意位置处的钢筋应力,以上两个公式即是解法1与解法2的计算基础。
可采用近似的线性关系,即公式(3-15-4)。按上述两个公式可以计算截面任意位置处的钢筋应力,以上两个公式即是解法1与解法2的计算基础。
更进一步,当混凝土受压区高度按规范公式(7.2.1-2)计算,在本题的情况下有:

于是正截面受弯承载力可按规范公式(7.2.5)计算。即得到:
M=f A
A (h-a
(h-a -a′
-a′ ),此即解法3的计算基础。
),此即解法3的计算基础。
如果本题不能正确计算,说明考生在钢筋混凝土构件正截面受弯承载力计算基础知识方面尚需补课。
在对称配筋情况下,受压钢筋应力不可能达到f′
 。此时某钢筋应力可按《混凝土结构设计规范》公式(7.1.5-1)计算:
。此时某钢筋应力可按《混凝土结构设计规范》公式(7.1.5-1)计算: (3-15-1)
(3-15-1)式中,h′
 为纵向受压钢筋截面重心至截面受压边缘的距离,h′
为纵向受压钢筋截面重心至截面受压边缘的距离,h′ =a′
=a′ =40mm。
=40mm。σ′
 =2.0×10
=2.0×10 ×0.0033×[(0.8×40/x)-1]=660[(32/x)-1]
×0.0033×[(0.8×40/x)-1]=660[(32/x)-1]根据内力平衡条件可以写出:
 (3-15-2)
(3-15-2)1.0×11.9×200x=300×628+660[(32/x)-1]×628
化简后得到
x
 +95x-5573=0
+95x-5573=0x=
 =41mm
=41mmσ′
 =660[(32/41)-1]=-145N/mm
=660[(32/41)-1]=-145N/mm
根据对A
 取矩的平衡关系:
取矩的平衡关系: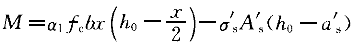 (3-15-3)
(3-15-3)=1.0×11.9×200×41×(360-41/2)+145×628×(360-40)
=62267610N·mm=62.268kN·m
(2)解法2
受压钢筋的应力按规范近似公式(7.1.5-3)计算:
 (3-15-4)
(3-15-4)式中

于是
σ′
 =300/0.55-0.8[(x/40)-0.8]=-30x+960
=300/0.55-0.8[(x/40)-0.8]=-30x+960根据式(3-15-2)
1.0×11.9×200x=300×628+(-30x+960)×628
σ′
 =-30×37.3+960=-159N/mm
=-30×37.3+960=-159N/mm
又从式(3-15-3)得:
M=1.0×11.9×200×37.3×[360-(1/2)×37.3]+159×628×320
=62255644N·mm=62.256kN·m
(3)解法3
按近似方法计算,取x=2a′
 =80mm
=80mmM=300×628×320=60288000N·mm=60.288kN·m
从以上计算结果可以看出,解法1与解法2所得的弯矩值基本相同,说明了采用近似公式(3-15-4)计算钢筋应力的合理性;解法3虽弯矩值略有差异,但与解法1相比,其误差只有3.18%,可以接受,所以按上述三种方法计算都是合理的,选项A是正确的。
选项B则是错误地取用f
 =360N/mm
=360N/mm 计算所得结果,选项C系按水平梁计算,选项D是计算错误,都是不正确的。
计算所得结果,选项C系按水平梁计算,选项D是计算错误,都是不正确的。【点评】:公式(3-15-1)是根据中和轴高度等于x/β
 、混凝土极限压应变ε
、混凝土极限压应变ε ,按平截面假定导出的求钢筋应力的一般公式。为了简化计算,避免在正截面承载力计算中出现求解二次方程,根据试验资料的分析,考虑到ξ=ξ
,按平截面假定导出的求钢筋应力的一般公式。为了简化计算,避免在正截面承载力计算中出现求解二次方程,根据试验资料的分析,考虑到ξ=ξ 及ξ=β
及ξ=β 的边界条件,σ
的边界条件,σ 与x/h
与x/h 可采用近似的线性关系,即公式(3-15-4)。按上述两个公式可以计算截面任意位置处的钢筋应力,以上两个公式即是解法1与解法2的计算基础。
可采用近似的线性关系,即公式(3-15-4)。按上述两个公式可以计算截面任意位置处的钢筋应力,以上两个公式即是解法1与解法2的计算基础。更进一步,当混凝土受压区高度按规范公式(7.2.1-2)计算,在本题的情况下有:

于是正截面受弯承载力可按规范公式(7.2.5)计算。即得到:
M=f
 A
A (h-a
(h-a -a′
-a′ ),此即解法3的计算基础。
),此即解法3的计算基础。如果本题不能正确计算,说明考生在钢筋混凝土构件正截面受弯承载力计算基础知识方面尚需补课。
