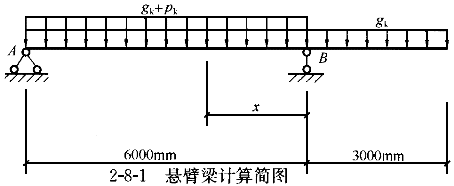
某钢筋混凝土悬臂梁(图2-8-1),其上作用的永久荷载标准值g =20kN/m,活荷载标准值p
=20kN/m,活荷载标准值p =12kN,/m(组合值系数0.7)。问AB跨跨中最大弯矩设计值与下列哪一个数值最接近?
=12kN,/m(组合值系数0.7)。问AB跨跨中最大弯矩设计值与下列哪一个数值最接近?
 =20kN/m,活荷载标准值p
=20kN/m,活荷载标准值p =12kN,/m(组合值系数0.7)。问AB跨跨中最大弯矩设计值与下列哪一个数值最接近?
=12kN,/m(组合值系数0.7)。问AB跨跨中最大弯矩设计值与下列哪一个数值最接近?
正确答案:
A
答案解析:
【主要解答过程如下】:(1)由永久荷载效应控制的组合
永久荷载设计值g=1.35×20=27kN/m
可变荷载设计值p=1.4×0.7×12=11.76kN/m
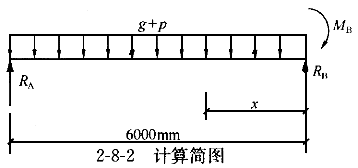
计算简图见图2-8-2。
M =-(1/2)gι
=-(1/2)gι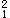 =-(1/2)×27×3
=-(1/2)×27×3 =-121.5kN·m
=-121.5kN·m
R =1/2(g+p)×6+M
=1/2(g+p)×6+M =(1/2)×38.76×6+121.5/6=136.53kN
=(1/2)×38.76×6+121.5/6=136.53kN
M =136.53x-(1/2)×38.76x
=136.53x-(1/2)×38.76x -121.5
-121.5
dM /dx=0,x=136.53/38.76=3.522m
/dx=0,x=136.53/38.76=3.522m
M =136.53×3.522-(1/2)×38.76×3.522
=136.53×3.522-(1/2)×38.76×3.522 -121.5=118.96kN·m
-121.5=118.96kN·m
(2)由可变荷载效应控制的组合
永久荷载设计值g=1.2×20=24kN,/m
可变荷载设计值p=1.4×12=16.8kN/m
M =-(1/2)×24×3
=-(1/2)×24×3 =-108kN·m
=-108kN·m
R =(1/2)×24+16.8)×6+108/6=40.8×3+18=140.4kN
=(1/2)×24+16.8)×6+108/6=40.8×3+18=140.4kN
M =140.4x-(1/2)×40.8x
=140.4x-(1/2)×40.8x -108
-108
dM /dx=0,x=140.4/40.8=3.441m
/dx=0,x=140.4/40.8=3.441m
M =140.4×3.441-(1/2)×40.8×3々441
=140.4×3.441-(1/2)×40.8×3々441 -108=133.56kN·m
-108=133.56kN·m
(3)当永久荷载效应对结构有利时
根据《建筑结构荷载规范》3.2.4条,当永久荷载效应对结构有利时,荷载分项系数取1.0。
永久荷载设计值g=1.0×20=20kN/m
可变荷载设计值p=1.4×12=16.8kN/m
M =-(1/2)×20×3
=-(1/2)×20×3 =-90kN·m
=-90kN·m
R =(1/2)×(20+16.8)×6+90/6=36.8×3+15=125.4kN
=(1/2)×(20+16.8)×6+90/6=36.8×3+15=125.4kN
M =125.4x-(1/2)×36.8x
=125.4x-(1/2)×36.8x -90
-90
dM /dx=0,x=125.4/36.8=3.41m
/dx=0,x=125.4/36.8=3.41m
M =125.4×3.41-(1/2)×36.8×3.41
=125.4×3.41-(1/2)×36.8×3.41 -90=123.65kN·m
-90=123.65kN·m
所以跨中最大弯矩设计值应为133.56kN·m,即选项A。B为跨度中点的弯矩设计值,并非最大值;C为永久荷载的分项系数用错所得结果;D是无根据的。
【点评】:(1)在本题求解跨中最大弯矩设计值时,将荷载的分项系数、组合值系数一并代入,然后计算;这是因为如果不是这样,则不能精确得到跨中最大弯矩设计值所在点的位置,也就得不到相应的弯矩设计值,这也可以在上述三种荷载效应组合的结果看出,最大弯矩值所在点的位置并不一致。
(2)《建筑结构荷载规范》3.2.4条规定,当永久荷载效应对结构有利时,荷载分项系数取1.0;这是对整个永久荷载而言,对一个结构的整体,或对一根连续梁的整体均是如此,例如对一根连续梁,不能是其中的某一些跨,永久荷载的分项系数取1.0,而对另一些跨则取1.20。笔者在主编《混凝土结构设计规范算例》一书过程中,曾就此问题与有关专家专门讨论过,请考生千万注意,选项C的错误就在于此。
按照错误的方法,本题解答如下:
M =-1.0×20×3
=-1.0×20×3 =-90kN·m
=-90kN·m
R =1/2(1.2×20+1.4×12)×6+90/6=3×40.8+15=137.4kN
=1/2(1.2×20+1.4×12)×6+90/6=3×40.8+15=137.4kN
M =137.4x-(1/2)×40.8x
=137.4x-(1/2)×40.8x -90
-90
dM /dx=0,x=137.4/40.8=3.37m
/dx=0,x=137.4/40.8=3.37m
M =137.4×3.37-(1/2)×40.8×3.37
=137.4×3.37-(1/2)×40.8×3.37 -90=141.36kN·m
-90=141.36kN·m
这就是选项C的结果。
永久荷载设计值g=1.35×20=27kN/m
可变荷载设计值p=1.4×0.7×12=11.76kN/m
计算简图见图2-8-2。

M
 =-(1/2)gι
=-(1/2)gι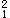 =-(1/2)×27×3
=-(1/2)×27×3 =-121.5kN·m
=-121.5kN·mR
 =1/2(g+p)×6+M
=1/2(g+p)×6+M =(1/2)×38.76×6+121.5/6=136.53kN
=(1/2)×38.76×6+121.5/6=136.53kNM
 =136.53x-(1/2)×38.76x
=136.53x-(1/2)×38.76x -121.5
-121.5dM
 /dx=0,x=136.53/38.76=3.522m
/dx=0,x=136.53/38.76=3.522mM
 =136.53×3.522-(1/2)×38.76×3.522
=136.53×3.522-(1/2)×38.76×3.522 -121.5=118.96kN·m
-121.5=118.96kN·m(2)由可变荷载效应控制的组合
永久荷载设计值g=1.2×20=24kN,/m
可变荷载设计值p=1.4×12=16.8kN/m
M
 =-(1/2)×24×3
=-(1/2)×24×3 =-108kN·m
=-108kN·mR
 =(1/2)×24+16.8)×6+108/6=40.8×3+18=140.4kN
=(1/2)×24+16.8)×6+108/6=40.8×3+18=140.4kNM
 =140.4x-(1/2)×40.8x
=140.4x-(1/2)×40.8x -108
-108dM
 /dx=0,x=140.4/40.8=3.441m
/dx=0,x=140.4/40.8=3.441mM
 =140.4×3.441-(1/2)×40.8×3々441
=140.4×3.441-(1/2)×40.8×3々441 -108=133.56kN·m
-108=133.56kN·m(3)当永久荷载效应对结构有利时
根据《建筑结构荷载规范》3.2.4条,当永久荷载效应对结构有利时,荷载分项系数取1.0。
永久荷载设计值g=1.0×20=20kN/m
可变荷载设计值p=1.4×12=16.8kN/m
M
 =-(1/2)×20×3
=-(1/2)×20×3 =-90kN·m
=-90kN·mR
 =(1/2)×(20+16.8)×6+90/6=36.8×3+15=125.4kN
=(1/2)×(20+16.8)×6+90/6=36.8×3+15=125.4kNM
 =125.4x-(1/2)×36.8x
=125.4x-(1/2)×36.8x -90
-90dM
 /dx=0,x=125.4/36.8=3.41m
/dx=0,x=125.4/36.8=3.41mM
 =125.4×3.41-(1/2)×36.8×3.41
=125.4×3.41-(1/2)×36.8×3.41 -90=123.65kN·m
-90=123.65kN·m所以跨中最大弯矩设计值应为133.56kN·m,即选项A。B为跨度中点的弯矩设计值,并非最大值;C为永久荷载的分项系数用错所得结果;D是无根据的。
【点评】:(1)在本题求解跨中最大弯矩设计值时,将荷载的分项系数、组合值系数一并代入,然后计算;这是因为如果不是这样,则不能精确得到跨中最大弯矩设计值所在点的位置,也就得不到相应的弯矩设计值,这也可以在上述三种荷载效应组合的结果看出,最大弯矩值所在点的位置并不一致。
(2)《建筑结构荷载规范》3.2.4条规定,当永久荷载效应对结构有利时,荷载分项系数取1.0;这是对整个永久荷载而言,对一个结构的整体,或对一根连续梁的整体均是如此,例如对一根连续梁,不能是其中的某一些跨,永久荷载的分项系数取1.0,而对另一些跨则取1.20。笔者在主编《混凝土结构设计规范算例》一书过程中,曾就此问题与有关专家专门讨论过,请考生千万注意,选项C的错误就在于此。
按照错误的方法,本题解答如下:
M
 =-1.0×20×3
=-1.0×20×3 =-90kN·m
=-90kN·mR
 =1/2(1.2×20+1.4×12)×6+90/6=3×40.8+15=137.4kN
=1/2(1.2×20+1.4×12)×6+90/6=3×40.8+15=137.4kNM
 =137.4x-(1/2)×40.8x
=137.4x-(1/2)×40.8x -90
-90dM
 /dx=0,x=137.4/40.8=3.37m
/dx=0,x=137.4/40.8=3.37mM
 =137.4×3.37-(1/2)×40.8×3.37
=137.4×3.37-(1/2)×40.8×3.37 -90=141.36kN·m
-90=141.36kN·m这就是选项C的结果。
