波长λ=6000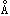
的单色光垂直入射到一光栅上，第二、第三级明条纹分别出现在sinφ=0．20与sinφ=0．30处，第四级缺级。求在-90°<φ<90°范围内，实际呈现的全部明条纹数目( )。
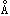的单色光垂直入射到一光栅上，第二、第三级明条纹分别出现在sinφ=0．20与sinφ=0．30处，第四级缺级。求在-90°<φ<90°范围内，实际呈现的全部明条纹数目( )。 正确答案：
A
答案解析：
【解析】由光栅方程(a+b)sinφ=kλ可知，对应于sinφ=0．20与sinφ=0．30处满足：0．20(a+b)=2×6000×10
；0．30(a+b)=3×6000×10；解得：a+b=6．0×10
因第四级缺级，故此须同时满足；(a+b)sinφ=kλ；asinφ=k′λ；解得：
a=(a+b/4)k′=1．5×10k′；取k′=1，得光栅狭缝的最小宽度为1．5×10m；由(a+b)sinφ=kλ；k=(a+b)sinφ/λ；当φ=π/2，对应k=k
；k=a+b/λ=6.0×10/6000×10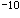
；
因±4，±8缺级，所以在-90°<φ＜90°范围内实际呈现的全部级数为k=0，±1，±2，±3，±5，±6，±7，±9，共15条明条纹(k=±10在k=±90°处，看不到)。
【点评】本题考察光栅缺级问题，这类问题求解步骤是：先由光栅方程(a+b)sinφ=从求出可能出现的明条纹数目，然后由缺级条件判断缺级数目，最后求出在-90°<φ<90°范围内实际呈现的全部级数或条纹数目。
；0．30(a+b)=3×6000×10；解得：a+b=6．0×10因第四级缺级，故此须同时满足；(a+b)sinφ=kλ；asinφ=k′λ；解得：
a=(a+b/4)k′=1．5×10
k′；取k′=1，得光栅狭缝的最小宽度为1．5×10m；由(a+b)sinφ=kλ；k=(a+b)sinφ/λ；当φ=π/2，对应k=k；k=a+b/λ=6.0×10/6000×10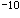；因±4，±8缺级，所以在-90°<φ＜90°范围内实际呈现的全部级数为k=0，±1，±2，±3，±5，±6，±7，±9，共15条明条纹(k=±10在k=±90°处，看不到)。
【点评】本题考察光栅缺级问题，这类问题求解步骤是：先由光栅方程(a+b)sinφ=从求出可能出现的明条纹数目，然后由缺级条件判断缺级数目，最后求出在-90°<φ<90°范围内实际呈现的全部级数或条纹数目。
