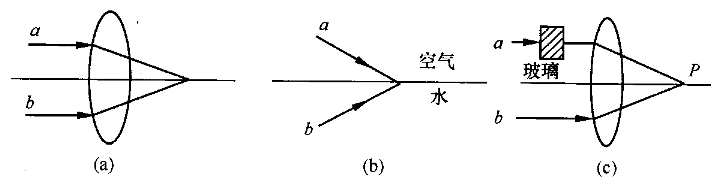
在图示的各种情况中,两条光线a和b开始时无光程差,判断相聚后是否有光程差,其光程差分别为:(设玻璃的宽度为l,折射率为n,空气的折射率为n =1,水的折射率为n
=1,水的折射率为n ,r是光线a和b的从出发点到相遇点的几何路程)( )。
,r是光线a和b的从出发点到相遇点的几何路程)( )。
 =1,水的折射率为n
=1,水的折射率为n ,r是光线a和b的从出发点到相遇点的几何路程)( )。
,r是光线a和b的从出发点到相遇点的几何路程)( )。
正确答案:
C
答案解析:
【解析】对图(a),由透镜的等光程性,图a中光程差值为零。对图(b),空气中:L =n
=n r=r(n
r=r(n 为空气的折射率,其值约等于1)水中:L
为空气的折射率,其值约等于1)水中:L =n
=n r(n
r(n 为水的折射率)则图(b)中光程的差值为L
为水的折射率)则图(b)中光程的差值为L =L
=L =(n
=(n -1)r;对图(c),光程差为:L
-1)r;对图(c),光程差为:L -L
-L =(r-ι)+ι·n-r=(n-1)ι;因此选答案C。
=(r-ι)+ι·n-r=(n-1)ι;因此选答案C。
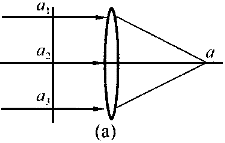
【点评】此题重点考察透镜的等光程性,以及光程的计算。在光的干涉实验中,常常需要用薄透镜将平行光会聚成一点,为了讨论会聚点的干涉情况,需要计算相干光在该点的光程差。由于透镜各处的厚度不相同,折射率也往往不知道,按光程的定义来计算有困难。下面我们讨论薄透镜的等光程性,提供一个简便计算的方法。几何光学告诉我们,平面光波通过透镜会聚在焦平面上时,叠加后总是形成亮点,如图所示。这个光学现象隐含着一个结论:与光束正交的波面上所有的同相点到透镜焦平面上像点的光程相同。即图(a)中的a 、a
、a 、a
、a 各点到像点a的光程相同;图(b)中的b
各点到像点a的光程相同;图(b)中的b 、b
、b 、b
、b 各点到b点的光程相同。正是由于光程相同,所以光传播到像点的相位变化也一样,因而在像点的各个光振动同相,才能干涉增强形成亮点。这个结果可以通过光程的定义来帮助理解。从波程来看,从同一波面到像点的光线中,过透镜中心的光线要短一些,过透镜边缘的光线要长一些;但从折射率来看。过透镜中心的光线要更多地经过玻璃,过透镜边缘的光线却很少通过玻璃,从波程和折射率这两个因素来分析,各条光线的光程相等是可以理解的。上述结论称为薄透镜的等光程性,即平行光经薄透镜会聚时各光线的光程相等。这提示我们,如果要计算两束平行光在会聚点的光程差,只需要在透镜前面垂直于光线作一个波面,只要知道两条光线在波面上的光程差,由于在会聚过程中各光线的光程相等,这个光程差将保持到会聚点。例如在图(a)表示的光路中,有两束平行光到达波面上a
各点到b点的光程相同。正是由于光程相同,所以光传播到像点的相位变化也一样,因而在像点的各个光振动同相,才能干涉增强形成亮点。这个结果可以通过光程的定义来帮助理解。从波程来看,从同一波面到像点的光线中,过透镜中心的光线要短一些,过透镜边缘的光线要长一些;但从折射率来看。过透镜中心的光线要更多地经过玻璃,过透镜边缘的光线却很少通过玻璃,从波程和折射率这两个因素来分析,各条光线的光程相等是可以理解的。上述结论称为薄透镜的等光程性,即平行光经薄透镜会聚时各光线的光程相等。这提示我们,如果要计算两束平行光在会聚点的光程差,只需要在透镜前面垂直于光线作一个波面,只要知道两条光线在波面上的光程差,由于在会聚过程中各光线的光程相等,这个光程差将保持到会聚点。例如在图(a)表示的光路中,有两束平行光到达波面上a 点和a
点和a 点后,经过透镜最终在会聚点a相遇,如果它们在a
点后,经过透镜最终在会聚点a相遇,如果它们在a 点和a
点和a 点的光程差是多少,则它们在a点的光程差也是多少。所以这个结论又叫做平行光经薄透镜会聚不附加光程差。
点的光程差是多少,则它们在a点的光程差也是多少。所以这个结论又叫做平行光经薄透镜会聚不附加光程差。

 =n
=n r=r(n
r=r(n 为空气的折射率,其值约等于1)水中:L
为空气的折射率,其值约等于1)水中:L =n
=n r(n
r(n 为水的折射率)则图(b)中光程的差值为L
为水的折射率)则图(b)中光程的差值为L =L
=L =(n
=(n -1)r;对图(c),光程差为:L
-1)r;对图(c),光程差为:L -L
-L =(r-ι)+ι·n-r=(n-1)ι;因此选答案C。
=(r-ι)+ι·n-r=(n-1)ι;因此选答案C。【点评】此题重点考察透镜的等光程性,以及光程的计算。在光的干涉实验中,常常需要用薄透镜将平行光会聚成一点,为了讨论会聚点的干涉情况,需要计算相干光在该点的光程差。由于透镜各处的厚度不相同,折射率也往往不知道,按光程的定义来计算有困难。下面我们讨论薄透镜的等光程性,提供一个简便计算的方法。几何光学告诉我们,平面光波通过透镜会聚在焦平面上时,叠加后总是形成亮点,如图所示。这个光学现象隐含着一个结论:与光束正交的波面上所有的同相点到透镜焦平面上像点的光程相同。即图(a)中的a
 、a
、a 、a
、a 各点到像点a的光程相同;图(b)中的b
各点到像点a的光程相同;图(b)中的b 、b
、b 、b
、b 各点到b点的光程相同。正是由于光程相同,所以光传播到像点的相位变化也一样,因而在像点的各个光振动同相,才能干涉增强形成亮点。这个结果可以通过光程的定义来帮助理解。从波程来看,从同一波面到像点的光线中,过透镜中心的光线要短一些,过透镜边缘的光线要长一些;但从折射率来看。过透镜中心的光线要更多地经过玻璃,过透镜边缘的光线却很少通过玻璃,从波程和折射率这两个因素来分析,各条光线的光程相等是可以理解的。上述结论称为薄透镜的等光程性,即平行光经薄透镜会聚时各光线的光程相等。这提示我们,如果要计算两束平行光在会聚点的光程差,只需要在透镜前面垂直于光线作一个波面,只要知道两条光线在波面上的光程差,由于在会聚过程中各光线的光程相等,这个光程差将保持到会聚点。例如在图(a)表示的光路中,有两束平行光到达波面上a
各点到b点的光程相同。正是由于光程相同,所以光传播到像点的相位变化也一样,因而在像点的各个光振动同相,才能干涉增强形成亮点。这个结果可以通过光程的定义来帮助理解。从波程来看,从同一波面到像点的光线中,过透镜中心的光线要短一些,过透镜边缘的光线要长一些;但从折射率来看。过透镜中心的光线要更多地经过玻璃,过透镜边缘的光线却很少通过玻璃,从波程和折射率这两个因素来分析,各条光线的光程相等是可以理解的。上述结论称为薄透镜的等光程性,即平行光经薄透镜会聚时各光线的光程相等。这提示我们,如果要计算两束平行光在会聚点的光程差,只需要在透镜前面垂直于光线作一个波面,只要知道两条光线在波面上的光程差,由于在会聚过程中各光线的光程相等,这个光程差将保持到会聚点。例如在图(a)表示的光路中,有两束平行光到达波面上a 点和a
点和a 点后,经过透镜最终在会聚点a相遇,如果它们在a
点后,经过透镜最终在会聚点a相遇,如果它们在a 点和a
点和a 点的光程差是多少,则它们在a点的光程差也是多少。所以这个结论又叫做平行光经薄透镜会聚不附加光程差。
点的光程差是多少,则它们在a点的光程差也是多少。所以这个结论又叫做平行光经薄透镜会聚不附加光程差。

