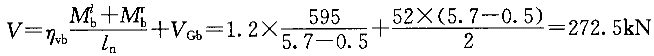19.《高规》6．2．5条规定，框架梁端部截面组合的剪力设计值
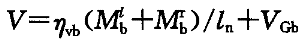
式中，M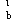
、M
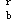分别为梁左、右端逆时针或顺时针方向截面组合的弯矩设计值。当抗震等级为一级且梁两端弯矩均为负弯矩时，绝对值较小一端的弯矩应取为零。
我的问题是：
(1)这里的"负弯矩"如何理解?
(2)计算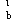M、M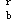时已经考虑了地震组合，即已有重力荷载代表值的效应在内了，为什么还要再加上v
?
(3)作用效应组合有许多种，公式中的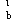M、M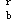是不是要求为同一个组合?
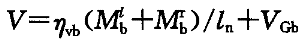
式中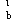，M
、M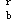分别为梁左、右端逆时针或顺时针方向截面组合的弯矩设计值。当抗震等级为一级且梁两端弯矩均为负弯矩时，绝对值较小一端的弯矩应取为零。我的问题是：
(1)这里的"负弯矩"如何理解?
(2)计算M
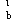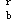、M时已经考虑了地震组合，即已有重力荷载代表值的效应在内了，为什么还要再加上v?(3)作用效应组合有许多种，公式中的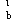M
、M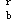是不是要求为同一个组合? 正确答案：
19.(1)事实上，这里弯矩的正负号规定与材料力学中相同，以梁下缘纤维受拉为正，图2-5-4中所示的为负弯矩。
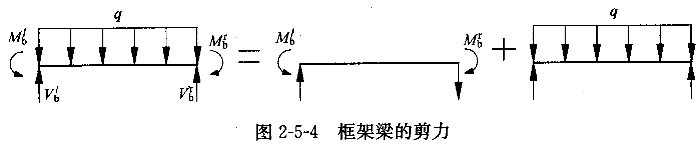
图2-5-4表示梁的受力可以分解为两种情况的叠加。今梁两端均为负弯矩，令M、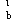
M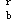仅表示数值大小，则由于梁端弯矩引起的剪力为
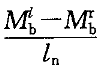，将绝对值较小的弯矩取为零，会导致剪力变大，按此变大的剪力设计会具有更高的安全度。
(2)由图2-5-4的计算原理可知，在计算出杆端力之后，需要考虑杆上的局部荷载才能得到正确的内力。
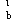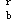(3)从概念上看，M、M应处于同一种荷载组合。王亚勇、戴国莹主编《建筑抗震设计规范算例》(中国建筑工业出版社，2006)57页、89页的算例由于用SATWE直接计
算出了梁端的剪力标准值，因此，采用效应组合方式直接算出了最不利的梁端剪力而没有
"显式"用到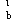M、M。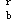
为加深认识，今举一例说明：
某框架梁，跨长5．7m，柱宽500mm，梁截面b×h=250mm×600mm，抗震等级为二级。作用于梁上的重力荷载设计值为52kN／m。在重力荷载和地震作用组合下，梁左支座柱边弯矩M
=210kNm，-M=-420kNm；梁右支座柱边弯矩M=175kNm，-M=-360kNm。梁跨中最大弯矩M=180kNm，梁中最大剪M=230kN。
要求：确定配置箍筋时的剪力设计值。
解：依据《高规》6．2．5条，框架梁剪力设计值按照下式计算
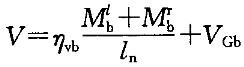
计算剪力的本质是梁的受力平衡，即弯矩顺时针、逆时针方向合力为零，由于顺时针、逆时针本身已经考虑了弯矩的符号，同时，剪力的正、负号并不影响配筋，故计算一律取弯矩的绝对值进行。于是
顺时针时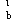M+M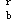=210+360=570kNm
逆时针时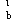M+M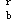=420+175=595kNm
取二者较大者计算剪力，从而
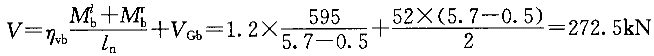
图2-5-4表示梁的受力可以分解为两种情况的叠加。今梁两端均为负弯矩，令M
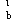、M
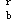仅表示数值大小，则由于梁端弯矩引起的剪力为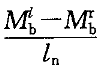，将绝对值较小的弯矩取为零，会导致剪力变大，按此变大的剪力设计会具有更高的安全度。(2)由图2-5-4的计算原理可知，在计算出杆端力之后，需要考虑杆上的局部荷载才能得到正确的内力。
(3)从概念上看，M
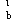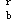、M应处于同一种荷载组合。王亚勇、戴国莹主编《建筑抗震设计规范算例》(中国建筑工业出版社，2006)57页、89页的算例由于用SATWE直接计算出了梁端的剪力标准值，因此，采用效应组合方式直接算出了最不利的梁端剪力而没有
"显式"用到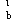M
、M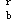。为加深认识，今举一例说明：
某框架梁，跨长5．7m，柱宽500mm，梁截面b×h=250mm×600mm，抗震等级为二级。作用于梁上的重力荷载设计值为52kN／m。在重力荷载和地震作用组合下，梁左支座柱边弯矩M
=210kNm，-M=-420kNm；梁右支座柱边弯矩M=175kNm，-M=-360kNm。梁跨中最大弯矩M=180kNm，梁中最大剪M=230kN。要求：确定配置箍筋时的剪力设计值。
解：依据《高规》6．2．5条，框架梁剪力设计值按照下式计算
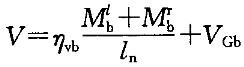
计算剪力的本质是梁的受力平衡，即弯矩顺时针、逆时针方向合力为零，由于顺时针、逆时针本身已经考虑了弯矩的符号，同时，剪力的正、负号并不影响配筋，故计算一律取弯矩的绝对值进行。于是
顺时针时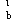M
+M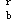=210+360=570kNm逆时针时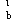M
+M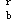=420+175=595kNm取二者较大者计算剪力，从而
