4.对《钢规》3.2.8条所规定的简化二阶效应计算,能否给出一个示例?
正确答案:
4.下面是笔者根据对规范的认识所做的一个算例。
某冶炼车间的操作平台,梁跨度9m,柱距5m,柱顶与梁铰接,柱底与基础刚接,如图2-2-1所示。全部平台结构的自重标准值为2kN/m ,由检修材料产生的平台均布活荷载标准值为24kN/m
,由检修材料产生的平台均布活荷载标准值为24kN/m ,每片框架承受的水平活荷载标准值为60kN。在平台梁的跨内设有检修用的单轨吊车,其集中荷载标准值为90kN。沿各列柱的纵向均设置有柱间支撑,平台面有密布铺板可靠连接。已知平台结构全部采用Q235钢,边列柱截面为1400×250×10)<20(I=4.0X10
,每片框架承受的水平活荷载标准值为60kN。在平台梁的跨内设有检修用的单轨吊车,其集中荷载标准值为90kN。沿各列柱的纵向均设置有柱间支撑,平台面有密布铺板可靠连接。已知平台结构全部采用Q235钢,边列柱截面为1400×250×10)<20(I=4.0X10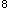 mm
mm ),中列柱截面为1500×250×12×25(I
),中列柱截面为1500×250×12×25(I =7.97×10
=7.97×10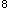 mm
mm )。要求:计算边柱柱底截面的轴力N和弯矩M。
)。要求:计算边柱柱底截面的轴力N和弯矩M。

解:依据《荷载规范》3.2.5条,采用简化组合,荷载效应取下列组合的最不利者:

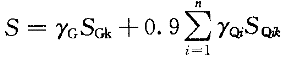

今只是示例,取第2种进行计算。
依据《荷载规范》3.2.5条,取自重分项系数1.2,单轨吊分项系数1.4,检修材料分项系数1.3。再根据《钢规》3.2.4条,检修材料对柱计算时采用0.75的折减系数。
边柱承受重力荷载设计值:
N=1.2×2×(4.5×5)+0.9×[0.75×1.3×24×(4.5×5)+1.4×50)]
=590.85kN
上式中的50,为单轨吊对边柱的压力,由杠杆原理得到。
中柱承受重力荷载设计值:
N=1.2×2×(9.0×5)+0.9×[0.75×1.3×24×(9.0×5)+1.4×80)]
=1156.5kN
∑N=2×590.85+1156.5=2338.2kN
一层水平荷载设计值:
∑H=0.9×1.4+60=75.6kN
依据《钢规》附录A.2.1条, ,于是,有
,于是,有
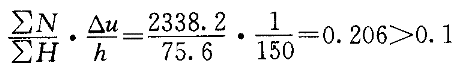
故宜采用二阶弹性分析。
假想水平力为:

将H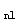 =9.35kN和H
=9.35kN和H =75.6kN叠加,得到横向力为84.95kN。在此横向力作用下,无侧移时,边柱柱底弯矩M
=75.6kN叠加,得到横向力为84.95kN。在此横向力作用下,无侧移时,边柱柱底弯矩M =0;有侧移时,边柱柱底弯矩:
=0;有侧移时,边柱柱底弯矩:

上式计算时,假定弯矩在各柱间按照刚度分配。
在水平力作用下柱顶侧移:
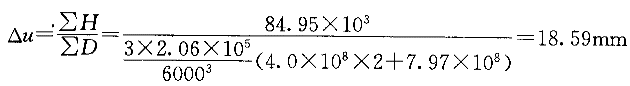
式中,D为柱顶发生单位侧移所需要的水平力,对下端固定,上端铰接柱, 。
。
于是,弯矩增大系数:
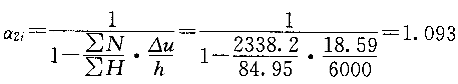
从而,考虑二阶效应时,边柱的柱底弯矩为:
MⅡ=M +α
+α M
M =0+1.093×140.3=153.3kN?m
=0+1.093×140.3=153.3kN?m
某冶炼车间的操作平台,梁跨度9m,柱距5m,柱顶与梁铰接,柱底与基础刚接,如图2-2-1所示。全部平台结构的自重标准值为2kN/m
 ,由检修材料产生的平台均布活荷载标准值为24kN/m
,由检修材料产生的平台均布活荷载标准值为24kN/m ,每片框架承受的水平活荷载标准值为60kN。在平台梁的跨内设有检修用的单轨吊车,其集中荷载标准值为90kN。沿各列柱的纵向均设置有柱间支撑,平台面有密布铺板可靠连接。已知平台结构全部采用Q235钢,边列柱截面为1400×250×10)<20(I=4.0X10
,每片框架承受的水平活荷载标准值为60kN。在平台梁的跨内设有检修用的单轨吊车,其集中荷载标准值为90kN。沿各列柱的纵向均设置有柱间支撑,平台面有密布铺板可靠连接。已知平台结构全部采用Q235钢,边列柱截面为1400×250×10)<20(I=4.0X10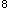 mm
mm ),中列柱截面为1500×250×12×25(I
),中列柱截面为1500×250×12×25(I =7.97×10
=7.97×10 mm
mm )。要求:计算边柱柱底截面的轴力N和弯矩M。
)。要求:计算边柱柱底截面的轴力N和弯矩M。
解:依据《荷载规范》3.2.5条,采用简化组合,荷载效应取下列组合的最不利者:

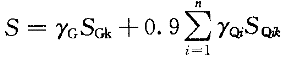

今只是示例,取第2种进行计算。
依据《荷载规范》3.2.5条,取自重分项系数1.2,单轨吊分项系数1.4,检修材料分项系数1.3。再根据《钢规》3.2.4条,检修材料对柱计算时采用0.75的折减系数。
边柱承受重力荷载设计值:
N=1.2×2×(4.5×5)+0.9×[0.75×1.3×24×(4.5×5)+1.4×50)]
=590.85kN
上式中的50,为单轨吊对边柱的压力,由杠杆原理得到。
中柱承受重力荷载设计值:
N=1.2×2×(9.0×5)+0.9×[0.75×1.3×24×(9.0×5)+1.4×80)]
=1156.5kN
∑N=2×590.85+1156.5=2338.2kN
一层水平荷载设计值:
∑H=0.9×1.4+60=75.6kN
依据《钢规》附录A.2.1条,
 ,于是,有
,于是,有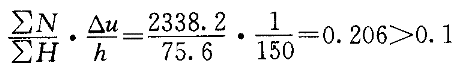
故宜采用二阶弹性分析。
假想水平力为:

将H
 =9.35kN和H
=9.35kN和H =75.6kN叠加,得到横向力为84.95kN。在此横向力作用下,无侧移时,边柱柱底弯矩M
=75.6kN叠加,得到横向力为84.95kN。在此横向力作用下,无侧移时,边柱柱底弯矩M =0;有侧移时,边柱柱底弯矩:
=0;有侧移时,边柱柱底弯矩:
上式计算时,假定弯矩在各柱间按照刚度分配。
在水平力作用下柱顶侧移:
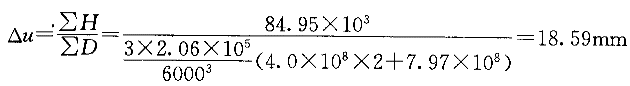
式中,D为柱顶发生单位侧移所需要的水平力,对下端固定,上端铰接柱,
 。
。于是,弯矩增大系数:
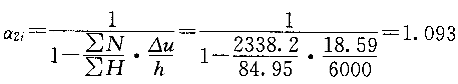
从而,考虑二阶效应时,边柱的柱底弯矩为:
MⅡ=M
 +α
+α M
M =0+1.093×140.3=153.3kN?m
=0+1.093×140.3=153.3kN?m 