两等跨等截面连续梁每跨跨长L=48m,采用先预制吊装后合龙固结的施工方法,左半跨徐变系数ψ (∞,t
(∞,t )=1,右边跨的徐变系数ψ
)=1,右边跨的徐变系数ψ (∞,t
(∞,t )=2,作用于桥上的均布恒载g=10kN/m(预制梁自重),E、I分别为该结构的弹性模量和截面抗弯惯性矩,如图1-74-1,当t=∞时中支点截面的徐变次弯矩与下列哪项数值最接近?
)=2,作用于桥上的均布恒载g=10kN/m(预制梁自重),E、I分别为该结构的弹性模量和截面抗弯惯性矩,如图1-74-1,当t=∞时中支点截面的徐变次弯矩与下列哪项数值最接近?

 (∞,t
(∞,t )=1,右边跨的徐变系数ψ
)=1,右边跨的徐变系数ψ (∞,t
(∞,t )=2,作用于桥上的均布恒载g=10kN/m(预制梁自重),E、I分别为该结构的弹性模量和截面抗弯惯性矩,如图1-74-1,当t=∞时中支点截面的徐变次弯矩与下列哪项数值最接近?
)=2,作用于桥上的均布恒载g=10kN/m(预制梁自重),E、I分别为该结构的弹性模量和截面抗弯惯性矩,如图1-74-1,当t=∞时中支点截面的徐变次弯矩与下列哪项数值最接近?
正确答案:
B
答案解析:
【主要解答过程如下】:(1)选取从跨中断开的两跨简支梁作为基本结构,由于合龙前,该截面的弯矩为零,合龙固结后该截面将产生徐变次弯矩。
(2)根据结构力学原理,在赘余联系处施加一对赘余力,即随时间t变化的待定徐变次弯矩M ,计算简图如图1-74-2所示。
,计算简图如图1-74-2所示。

(3)计算老化系数及换算弹性模量:
ρ (∞,t
(∞,t )=1/1-e
)=1/1-e -1/ψ
-1/ψ =1/1-e
=1/1-e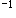 -1/1=0.582
-1/1=0.582
ρ (∞,t
(∞,t )=1/1-e
)=1/1-e -1/ψ
-1/ψ =1/1-e
=1/1-e -1/2=0.657
-1/2=0.657
E =E/ψ
=E/ψ (∞,t
(∞,t )=E,E
)=E,E =E/ψ
=E/ψ (∞,t
(∞,t )=E/2=0.5E
)=E/2=0.5E
E =E/[1+ρ
=E/[1+ρ (∞,t
(∞,t )ψ
)ψ (∞,t
(∞,t )]=E/[1+0.582×1]=0.632E
)]=E/[1+0.582×1]=0.632E
E =E/[1+ρ
=E/[1+ρ (∞,t
(∞,t )ψ
)ψ (∞,t
(∞,t )]=E/[1+0.582×2]=0.432E
)]=E/[1+0.582×2]=0.432E
(4)计算常变位和载变位(图乘法):
 =1/E
=1/E I/1[(1/2)×1×48×(2/3)]+1/E
I/1[(1/2)×1×48×(2/3)]+1/E I[(1/2)×48×(2/3)]=16/0.632EI=16/0.432EI
I[(1/2)×48×(2/3)]=16/0.632EI=16/0.432EI
=62.35/EI
 =1/E
=1/E I
I×48×(1/8)×10×48[http://cdn.laixue.com/exam/20405168/TestImages/~2.gif) ×(1/2)]+1/E
×(1/2)]+1/E I
I×48×(1/8)×10[http://cdn.laixue.com/exam/20405168/TestImages/~2.gif) ×(1/2)]
×(1/2)]
=138240/EI
(5)解力法方程:
 M
M +
+ =0
=0
62.35/EIM +138240/EI=0
+138240/EI=0
M =-2217kN·m即为B项数值。
=-2217kN·m即为B项数值。
(2)根据结构力学原理,在赘余联系处施加一对赘余力,即随时间t变化的待定徐变次弯矩M
 ,计算简图如图1-74-2所示。
,计算简图如图1-74-2所示。
(3)计算老化系数及换算弹性模量:
ρ
 (∞,t
(∞,t )=1/1-e
)=1/1-e -1/ψ
-1/ψ =1/1-e
=1/1-e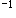 -1/1=0.582
-1/1=0.582ρ
 (∞,t
(∞,t )=1/1-e
)=1/1-e -1/ψ
-1/ψ =1/1-e
=1/1-e -1/2=0.657
-1/2=0.657E
 =E/ψ
=E/ψ (∞,t
(∞,t )=E,E
)=E,E =E/ψ
=E/ψ (∞,t
(∞,t )=E/2=0.5E
)=E/2=0.5EE
 =E/[1+ρ
=E/[1+ρ (∞,t
(∞,t )ψ
)ψ (∞,t
(∞,t )]=E/[1+0.582×1]=0.632E
)]=E/[1+0.582×1]=0.632EE
 =E/[1+ρ
=E/[1+ρ (∞,t
(∞,t )ψ
)ψ (∞,t
(∞,t )]=E/[1+0.582×2]=0.432E
)]=E/[1+0.582×2]=0.432E(4)计算常变位和载变位(图乘法):
 =1/E
=1/E I/1[(1/2)×1×48×(2/3)]+1/E
I/1[(1/2)×1×48×(2/3)]+1/E I[(1/2)×48×(2/3)]=16/0.632EI=16/0.432EI
I[(1/2)×48×(2/3)]=16/0.632EI=16/0.432EI=62.35/EI
 =1/E
=1/E I
I×48×(1/8)×10×48[http://cdn.laixue.com/exam/20405168/TestImages/~2.gif) ×(1/2)]+1/E
×(1/2)]+1/E I
I×48×(1/8)×10[http://cdn.laixue.com/exam/20405168/TestImages/~2.gif) ×(1/2)]
×(1/2)]=138240/EI
(5)解力法方程:
 M
M +
+ =0
=062.35/EIM
 +138240/EI=0
+138240/EI=0M
 =-2217kN·m即为B项数值。
=-2217kN·m即为B项数值。