如图1-72-1所示某钢筋混凝土圆筒形塔结构,建造于中等城市郊区。该塔结构质量沿高度按连续规律变化,塔体表面光滑,其混凝土强度等级为C25,E =280×10
=280×10 kN/㎡,钢筋采用HRB400级。基本风压w
kN/㎡,钢筋采用HRB400级。基本风压w =0.45kN/㎡,问在风荷载作用下该塔底部截面的弯矩设计值(kN·m)与下列哪项值最为接近?(提示:本题按《荷载规范》计算。)
=0.45kN/㎡,问在风荷载作用下该塔底部截面的弯矩设计值(kN·m)与下列哪项值最为接近?(提示:本题按《荷载规范》计算。)

 =280×10
=280×10 kN/㎡,钢筋采用HRB400级。基本风压w
kN/㎡,钢筋采用HRB400级。基本风压w =0.45kN/㎡,问在风荷载作用下该塔底部截面的弯矩设计值(kN·m)与下列哪项值最为接近?(提示:本题按《荷载规范》计算。)
=0.45kN/㎡,问在风荷载作用下该塔底部截面的弯矩设计值(kN·m)与下列哪项值最为接近?(提示:本题按《荷载规范》计算。)
正确答案:
A
答案解析:
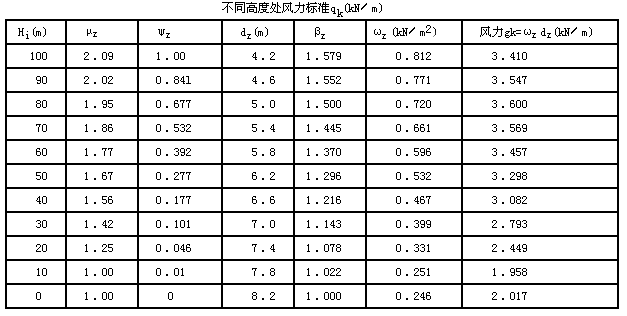
【主要解答过程如下】:(1)本工程建造在中等城市郊区,按《荷载规范》第7.2.1条规定,地面粗糙度属于B类,不同高度的风压高度变化系数μ ,由《荷载规范》表7.2.1查出,如表所列。
,由《荷载规范》表7.2.1查出,如表所列。
(2)风荷载体型系数μ ,本工程属悬臂结构,截面为圆形,表面光滑(△≈0)情况,H/d=100/4.2=23.8,可由《荷载规范》表7.3.1项次36查得,μ
,本工程属悬臂结构,截面为圆形,表面光滑(△≈0)情况,H/d=100/4.2=23.8,可由《荷载规范》表7.3.1项次36查得,μ =0.547。
=0.547。
(3)风振系数β :按《荷载规范》第7.4.2条式(7.4.2)确定:
:按《荷载规范》第7.4.2条式(7.4.2)确定:
β =1+ξvψ
=1+ξvψ /μ
/μ
结构基本自振周期参照《荷载规范》附录E第E.1.2条式(E.1.2-2)确定。
T =0.41+0.001H
=0.41+0.001H /d=0.41+0.001×(100
/d=0.41+0.001×(100 /6.2)=2.02s
/6.2)=2.02s
其中d为半高度处截面的外径,d=4.2+8.2/2=6.2m。
基本风压ω =0.45kN/㎡,ω
=0.45kN/㎡,ω T
T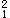 =0.45×2.02
=0.45×2.02 =1.836
=1.836
查《荷载规范》第7.4.3得脉动增大系数ξ=1.524
查《荷载规范》第7.4.4-1得脉动影响系数v=0.90但由于本题的塔结构迎风面和侧风面的宽度沿高度按直线变化,且质量沿高度按直线规律变化,因此根据《荷载规范》第7.4.4条第2款规定对表7.4.4-1中的脉动影响系数应再乘以θ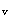 及θ
及θ 。今θ
。今θ =d
=d /d
/d =d
=d /8.2,其中d
/8.2,其中d 为在z高度处的塔直径;θ
为在z高度处的塔直径;θ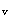 应按表7.4.4-2查得:θ
应按表7.4.4-2查得:θ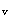 =1.72(因d
=1.72(因d /d
/d =4.2/8.2=0.512)即v=0.9×1.72×d
=4.2/8.2=0.512)即v=0.9×1.72×d /8.2=0.189d
/8.2=0.189d 。
。
因此,不同高度处的风振系数:
β =1+ξvψ
=1+ξvψ /μ
/μ =1+1.524×0.189(d
=1+1.524×0.189(d ψ
ψ /μ
/μ )=1+0.288d
)=1+0.288d ψ
ψ /μ
/μ
(4)在不同高度处的风荷载标准值毗:
ω =β
=β μ
μ μ
μ ω
ω =0.547×0.45β
=0.547×0.45β μ
μ =0.246β
=0.246β μ
μ
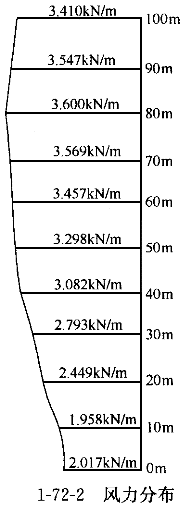
(5)为计算塔体在风荷载作用下底部截面的弯矩,应先求出作用在塔身的风力。将塔身沿高度分为10段,每段高10m,其风力标准值可求得如表所列及图所示。其中ψ 值查自《荷载规范》附录F的表F.1.3(根据B
值查自《荷载规范》附录F的表F.1.3(根据B /B
/B 即D
即D /d
/d =0.512查得)
=0.512查得)
(6)求塔底部截面的弯矩设计值M:M=γ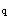 M
M =1.4Mk
=1.4Mk
M=1.4×[3.410×10×95+(3.547-3.410)×(10/2)×(90+10/3)
+3.547×10×85+(3.60-3.547)×(10/2)×(80+10/3)
+3.569×10×75+(3.60-3.569)×(10/2)×(70+20/3)
+3.457×10×65+(3.569-3.457)×(10/2)×(60+20/3)
+3.298×10×55+(3.457-3.298)×(10/2)×(50+20/3)
+3.082×10×45+(3.298-3.082)×(10/2)×(40+20/3)
+2.793×10×35+(3.082-2.793)×(10/2)×(30+20/3)
+2.449×10×25+(2.793-2.449)×(10/2)×(20+20/3)
+1.958×10×15+(2.449-1.958)×(10/2)×(10+20/3)
+1.958×10×5+(2.017-1.958)×(10/2)×(10/3)]
=1.4[3239.50+63.93+3014.95+22.08+2676.75+11.88+2247.05
+37.334-1813.904-45.054-1386.904-50.404-977.554-52.994-612.25
+45.874-293.704-40.924-293.704-40.924-97.904-0.98]
=23893.1kN·m
与A项最为接近。
【点评】:在计算中应注意此类结构的脉动影响系数应乘以修正系数钆及巩。结构工程师对此可能忽视。
 ,由《荷载规范》表7.2.1查出,如表所列。
,由《荷载规范》表7.2.1查出,如表所列。(2)风荷载体型系数μ
 ,本工程属悬臂结构,截面为圆形,表面光滑(△≈0)情况,H/d=100/4.2=23.8,可由《荷载规范》表7.3.1项次36查得,μ
,本工程属悬臂结构,截面为圆形,表面光滑(△≈0)情况,H/d=100/4.2=23.8,可由《荷载规范》表7.3.1项次36查得,μ =0.547。
=0.547。(3)风振系数β
 :按《荷载规范》第7.4.2条式(7.4.2)确定:
:按《荷载规范》第7.4.2条式(7.4.2)确定:β
 =1+ξvψ
=1+ξvψ /μ
/μ
结构基本自振周期参照《荷载规范》附录E第E.1.2条式(E.1.2-2)确定。
T
 =0.41+0.001H
=0.41+0.001H /d=0.41+0.001×(100
/d=0.41+0.001×(100 /6.2)=2.02s
/6.2)=2.02s其中d为半高度处截面的外径,d=4.2+8.2/2=6.2m。
基本风压ω
 =0.45kN/㎡,ω
=0.45kN/㎡,ω T
T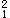 =0.45×2.02
=0.45×2.02 =1.836
=1.836查《荷载规范》第7.4.3得脉动增大系数ξ=1.524
查《荷载规范》第7.4.4-1得脉动影响系数v=0.90但由于本题的塔结构迎风面和侧风面的宽度沿高度按直线变化,且质量沿高度按直线规律变化,因此根据《荷载规范》第7.4.4条第2款规定对表7.4.4-1中的脉动影响系数应再乘以θ
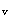 及θ
及θ 。今θ
。今θ =d
=d /d
/d =d
=d /8.2,其中d
/8.2,其中d 为在z高度处的塔直径;θ
为在z高度处的塔直径;θ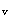 应按表7.4.4-2查得:θ
应按表7.4.4-2查得:θ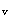 =1.72(因d
=1.72(因d /d
/d =4.2/8.2=0.512)即v=0.9×1.72×d
=4.2/8.2=0.512)即v=0.9×1.72×d /8.2=0.189d
/8.2=0.189d 。
。因此,不同高度处的风振系数:
β
 =1+ξvψ
=1+ξvψ /μ
/μ =1+1.524×0.189(d
=1+1.524×0.189(d ψ
ψ /μ
/μ )=1+0.288d
)=1+0.288d ψ
ψ /μ
/μ
(4)在不同高度处的风荷载标准值毗:
ω
 =β
=β μ
μ μ
μ ω
ω =0.547×0.45β
=0.547×0.45β μ
μ =0.246β
=0.246β μ
μ
(5)为计算塔体在风荷载作用下底部截面的弯矩,应先求出作用在塔身的风力。将塔身沿高度分为10段,每段高10m,其风力标准值可求得如表所列及图所示。其中ψ
 值查自《荷载规范》附录F的表F.1.3(根据B
值查自《荷载规范》附录F的表F.1.3(根据B /B
/B 即D
即D /d
/d =0.512查得)
=0.512查得)

(6)求塔底部截面的弯矩设计值M:M=γ
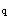 M
M =1.4Mk
=1.4MkM=1.4×[3.410×10×95+(3.547-3.410)×(10/2)×(90+10/3)
+3.547×10×85+(3.60-3.547)×(10/2)×(80+10/3)
+3.569×10×75+(3.60-3.569)×(10/2)×(70+20/3)
+3.457×10×65+(3.569-3.457)×(10/2)×(60+20/3)
+3.298×10×55+(3.457-3.298)×(10/2)×(50+20/3)
+3.082×10×45+(3.298-3.082)×(10/2)×(40+20/3)
+2.793×10×35+(3.082-2.793)×(10/2)×(30+20/3)
+2.449×10×25+(2.793-2.449)×(10/2)×(20+20/3)
+1.958×10×15+(2.449-1.958)×(10/2)×(10+20/3)
+1.958×10×5+(2.017-1.958)×(10/2)×(10/3)]
=1.4[3239.50+63.93+3014.95+22.08+2676.75+11.88+2247.05
+37.334-1813.904-45.054-1386.904-50.404-977.554-52.994-612.25
+45.874-293.704-40.924-293.704-40.924-97.904-0.98]
=23893.1kN·m
与A项最为接近。
【点评】:在计算中应注意此类结构的脉动影响系数应乘以修正系数钆及巩。结构工程师对此可能忽视。
