如图2.2-6所示，S1和S2为两个相干波源，它们的振动方向均垂直于图面，发出波长为λ的简谐波，P点是两列波相遇区域中的一点，已知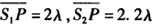
，两列波在P点发生相消干涉。若S
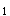的振动方程为y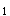=Acos［2πt+π/2］，则S
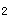的振动方程是( )。
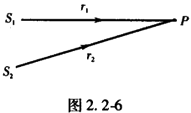
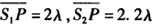，两列波在P点发生相消干涉。若S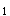的振动方程为y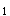=Acos［2πt+π/2］，则S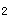的振动方程是( )。 - A. y=Acos［2πt一π/2］
- B. y=Acos［2πt-π］
- C. y=Acos［2πt+π/2］
- D. y=2Acos［2πt-0.1π］
正确答案：
D
答案解析：
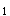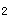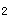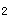由y表达式中ω=2π，可知周期T=1s，根据相干条件，设相干波源S的振动方程为y=Acos(2πt+
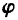)。再由波动方程一般式
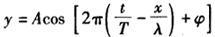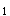，波源S和S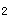传到P点的振动方程为
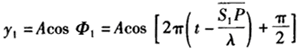
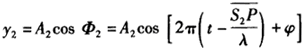
根据题意，两列波在P点发生相消干涉，应有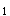φ-φ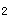=（2k+1）π，将
代入，解出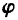=-0.2π-2kπ，如取|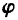|≤π，则k=0，有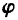=-0.1π，于是可得S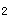的振动方程为y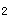=A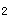cos(2πt-0.1π)。由于相消干涉只要求两振动反相位，不一定非要合振动为零，题中所给选项中只有(D)相位满足要求，所以正确答案应为(D)，此时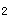A=2A。
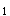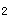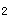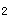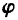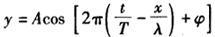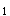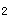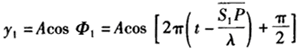
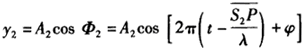
表达式中ω=2π，可知周期T=1s，根据相干条件，设相干波源S的振动方程为y=Acos(2πt+)。再由波动方程一般式，波源S和S传到P点的振动方程为根据题意，两列波在P点发生相消干涉，应有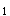φ
-φ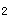=（2k+1）π，将代入，解出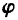=-0.2π-2kπ，如取|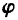|≤π，则k=0，有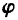=-0.1π，于是可得S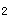的振动方程为y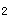=A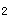cos(2πt-0.1π)。由于相消干涉只要求两振动反相位，不一定非要合振动为零，题中所给选项中只有(D)相位满足要求，所以正确答案应为(D)，此时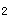A=2A。
